



Next: Nichtlineare Resonanzspektroskopie
Up: Steuerung mit Poincaré
Previous: Steuerung mit Poincaré
Das Rössler-System (1.3) erfüllt die Bedingungen des
letzten Abschnitts. Dazu wählt man als Poincaré
-Ebene 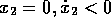 , weil
in diesem Bereich
, weil
in diesem Bereich  nahezu verschwindet (vgl. Abb. 1.6).
Die Dynamik auf dem Poincaré
-Schnitt kann also näherungsweise eindimensional
betrachtet werden. Außerdem hängt die Wiederkehrzeit zur Poincaré
-Ebene
in der Nähe des Attraktors nur schwach von
nahezu verschwindet (vgl. Abb. 1.6).
Die Dynamik auf dem Poincaré
-Schnitt kann also näherungsweise eindimensional
betrachtet werden. Außerdem hängt die Wiederkehrzeit zur Poincaré
-Ebene
in der Nähe des Attraktors nur schwach von  ab
(vgl. Abb. 5.2).
ab
(vgl. Abb. 5.2).

Auch der nächste  -Wert hängt nur sehr schwach vom Anfangswert von
-Wert hängt nur sehr schwach vom Anfangswert von  ab (vgl. Abb. 5.3).
Im folgenden wird deshalb die Abhängigkeit von der
ab (vgl. Abb. 5.3).
Im folgenden wird deshalb die Abhängigkeit von der  -Komponente
vernachlässigt.
Durch Anwendung numerischer Verfahren (vgl. Kapitel
2.2.2) erhält man Polynomapproximationen
für die Wiederkehrzeit und den nächsten
-Komponente
vernachlässigt.
Durch Anwendung numerischer Verfahren (vgl. Kapitel
2.2.2) erhält man Polynomapproximationen
für die Wiederkehrzeit und den nächsten  -Wert als
Funktion der Anfangswerte für
-Wert als
Funktion der Anfangswerte für  (Tabelle 5.1).
(Tabelle 5.1).


Diese Approximationen stellen das diskrete Modell des Rössler-Systems dar,
mit dem es nun gesteuert werden soll.
Als Solldynamik wurde eine periodische Dynamik des kontinuierlichen
Systems, also ein Fixpunkt in der Poincaré
-Ebene gewählt:

Dabei wurde für die Lage des Sollfixpunkts einmal  , zum
anderen
, zum
anderen  gewählt. Die Anwendung des Stabilitätskriteriums aus
den Gleichungen (5.12) bis (5.14) liefert
die Eigenwerte aus Tabelle 5.2. Eine stabile
rückkopplungsfreie Steuerung auf eine periodische Wunschdynamik ist
also für
gewählt. Die Anwendung des Stabilitätskriteriums aus
den Gleichungen (5.12) bis (5.14) liefert
die Eigenwerte aus Tabelle 5.2. Eine stabile
rückkopplungsfreie Steuerung auf eine periodische Wunschdynamik ist
also für  möglich. Für
möglich. Für  und
und  gibt es keinen
Bereich für
gibt es keinen
Bereich für  , in dem beide Eigenwerte betragsmäßig kleiner als eins
sind. Eine stabile Steuerung ist für diese Fälle also nicht zu erwarten.
, in dem beide Eigenwerte betragsmäßig kleiner als eins
sind. Eine stabile Steuerung ist für diese Fälle also nicht zu erwarten.

Abb. 5.4 zeigt die Wirkung der Anwendung
einer  -förmigen Steuerkraft auf das kontinuierliche System.
-förmigen Steuerkraft auf das kontinuierliche System.

Da bei realen Sytemen 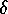 -förmige Kraftimpulse oft nicht angewendet werden
können, wird nun das Verhalten bei Steuerung mit Rechteckimpulsen
(Methode 2, Seite
-förmige Kraftimpulse oft nicht angewendet werden
können, wird nun das Verhalten bei Steuerung mit Rechteckimpulsen
(Methode 2, Seite  ) untersucht.
Abb. 5.5 zeigt für verschiedene Pulslängen dt
die mittlere quadratische Abweichung der gesteuerten
Dynamik von der Wunschdynamik
) untersucht.
Abb. 5.5 zeigt für verschiedene Pulslängen dt
die mittlere quadratische Abweichung der gesteuerten
Dynamik von der Wunschdynamik






Next: Nichtlineare Resonanzspektroskopie
Up: Steuerung mit Poincaré
Previous: Steuerung mit Poincaré
Werner Eberl
Fri Apr 14 00:36:50 MET DST 1995
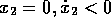 , weil
in diesem Bereich
, weil
in diesem Bereich  nahezu verschwindet (vgl. Abb. 1.6).
Die Dynamik auf dem Poincaré
-Schnitt kann also näherungsweise eindimensional
betrachtet werden. Außerdem hängt die Wiederkehrzeit zur Poincaré
-Ebene
in der Nähe des Attraktors nur schwach von
nahezu verschwindet (vgl. Abb. 1.6).
Die Dynamik auf dem Poincaré
-Schnitt kann also näherungsweise eindimensional
betrachtet werden. Außerdem hängt die Wiederkehrzeit zur Poincaré
-Ebene
in der Nähe des Attraktors nur schwach von  ab
(vgl. Abb. 5.2).
ab
(vgl. Abb. 5.2).





 -Wert hängt nur sehr schwach vom Anfangswert von
-Wert hängt nur sehr schwach vom Anfangswert von  ab (vgl. Abb.
ab (vgl. Abb.  -Komponente
vernachlässigt.
Durch Anwendung numerischer Verfahren (vgl. Kapitel
-Komponente
vernachlässigt.
Durch Anwendung numerischer Verfahren (vgl. Kapitel
 -Wert als
Funktion der Anfangswerte für
-Wert als
Funktion der Anfangswerte für  (Tabelle
(Tabelle 


 , zum
anderen
, zum
anderen  gewählt. Die Anwendung des Stabilitätskriteriums aus
den Gleichungen (
gewählt. Die Anwendung des Stabilitätskriteriums aus
den Gleichungen ( möglich. Für
möglich. Für  und
und  gibt es keinen
Bereich für
gibt es keinen
Bereich für  , in dem beide Eigenwerte betragsmäßig kleiner als eins
sind. Eine stabile Steuerung ist für diese Fälle also nicht zu erwarten.
, in dem beide Eigenwerte betragsmäßig kleiner als eins
sind. Eine stabile Steuerung ist für diese Fälle also nicht zu erwarten.

 -förmigen Steuerkraft auf das kontinuierliche System.
-förmigen Steuerkraft auf das kontinuierliche System.

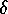 -förmige Kraftimpulse oft nicht angewendet werden
können, wird nun das Verhalten bei Steuerung mit Rechteckimpulsen
(Methode
-förmige Kraftimpulse oft nicht angewendet werden
können, wird nun das Verhalten bei Steuerung mit Rechteckimpulsen
(Methode 

