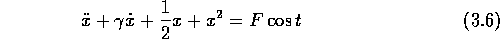




Die einfachste nichtlineare Näherung für jeden nichtlinearen, angetriebenen Schwinger ist der Helmholtz-Oszillator:
Mit wachsendem F gehen die zunächst periodischen Schwingungen
über ein Bifurkations-Szenario in chaotisches Verhalten über.
Der Übergang ins Chaos findet also genauso statt wie bei der
logistischen Abbildung. Die Frage ist nun, ob sich aus der
Differentialgleichung ( ) eine Abbildung errechnen
läßt, aus der man die analoge Bedeutung von F in
(
) eine Abbildung errechnen
läßt, aus der man die analoge Bedeutung von F in
( ) und a in (
) und a in ( ) entnehmen kann.
Dies ist in der Tat möglich [Ebe92],
sprengt aber den Rahmen dieses einführenden Werkes.
) entnehmen kann.
Dies ist in der Tat möglich [Ebe92],
sprengt aber den Rahmen dieses einführenden Werkes.
Vielmehr soll im nächsten Bild die qualitative Ähnlichkeit
des Chaos-Mechanismus beim Helmholtz-Oszillator mit dem der
Bäcker-Transformation ( ) offensichtlich werden.
) offensichtlich werden.
Das Prinzip ist immer: Strecken und Falten. Durch das Strecken entfernen sich benachbarte Anfangsbedingungen, sodaß man einen positiven Lyapunov-Exponenten erhält. Das Falten bewirkt, daß sie gesamte Bewegung auf einem Teil des Zustandsraumes beschränkt bleibt.
Ein gewisser Unterschied besteht darin, daß bei der Bäckertransformation das Volumen des Teiges konstant bleibt, während der Helmholtz-Oszillator dissipativ ist. Das Volumen des Helmoltz-Attraktors ist Null.
Obwohl die beiden Systeme zu verschiedenen Klassen dynamischer Systeme zählen, gelten bei beiden gleiche Prinzipien.
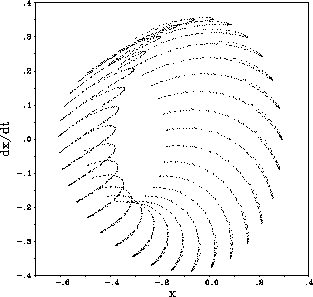
Figure: Stroboskopisch
(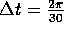 )
ausgewählte Punkte der Trajektorien des Helmholtz-Oszillators
(
)
ausgewählte Punkte der Trajektorien des Helmholtz-Oszillators
( ) für
) für 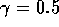 und
und 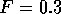 .
Deutlich zu sehen ist das Bäcker-Transformations-ähnliche
Verhalten, beim Umlauf im Uhrzeigersinn.
.
Deutlich zu sehen ist das Bäcker-Transformations-ähnliche
Verhalten, beim Umlauf im Uhrzeigersinn.