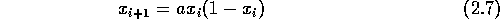
Es soll als Beispiel dazu das Verhalten der sog. logistischen Abbildung
untersucht werden. In den folgenden Abbildungen ist nach rechts
der Wert des Kontrollparameters a aufgetragen und nach oben
die Werte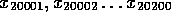 
, also 200 Werte
nach einer Einschwingdauer von 20000 Iterationen. Gestartet wurde
mit einem beliebigen ,,krummen`` Wert zwischen 0 und 1. Außerdem
ist der Lyapunov-Exponent als Funktion von a aufgetragen.
Figure: Bifurkationsdiagramm der logistischen Abbildung
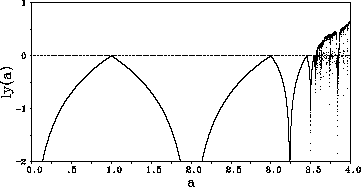
Figure: Lyapunov-Exponent der logistischen Abbildung
Für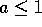 
konvergiert die Iteration gegen den Wert Null.
Im Bereich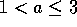 
konvergiert die Folge der 
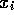nicht mehr
gegen Null, sondern gegen einen von a abhängigen Wert. Diese Werte
sind sog. Fixpunkte der Dynamik. Sie lassen sich durch Lösung
der Gleichung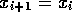 
bestimmen.
Bei a=3 wird der Fixpunkt instabil, d.h. wenn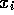 
knapp neben
dem Fixpunkt liegt, wird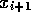 
weiter weg liegen.
Allerdings hat nun die Abbildung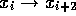 
zwei
stabile Fixpunkte. Für die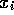 
bedeutet das, daß abwechselnd
der obere und der untere Punkt angenommen wird und die
Dynamik gegen dieses Hin-und-her konvergiert. Bei etwa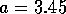 
werden auch diese Fixpunkte instabil, worauf sich eine
4-periodische Dynamik etabliert. Die Periode verdoppelt sich
nun immer weiter, wobei jedoch die Abstände in a-Richtung
immer kleiner werden, sodaß die Periode ,,
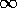`` bei einem
endlichen Wert erreicht wird.
Für noch größere Werte von a treten dann wieder periodische ,,Fenster`` auf, wobei jetzt auch Periodenlängen vorkommen, die sich nicht als Zweierpotenz schreiben lassen. Das breiteste Fenster hat die Periode 3.
