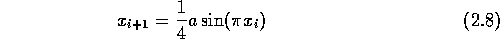




Die besondere Bedeutung des Übergangs ins Chaos durch fortgesetzte Periodenverdopplung (sog. Feigenbaum-Szenario) liegt darin, daß die spezielle Form der Funktion keine Rolle spielt, solange einige mathematische Bedingungen erfüllt sind. Z.B. liefert auch die Abbildung
ein Bifurkationsdiagramm, das dem der logistischen Abbildung sehr ähnlich ist. Die Übereinstimmung ist sogar quantitativ: Die Zahlenwerte der Verhältnisse der Abstände der Periodenverdopplung konvergieren gegen die gleichen Zahlen. Feigenbaum [Fei83] konnte zeigen, daß diese Zahlen universell für diese Klasse von Funktionen sind.
Damit ist es möglich, quantitative Angaben über das Verhaltens eines Systems zu machen, von dem die genaue Form seiner Dynamik nicht bekannt ist.
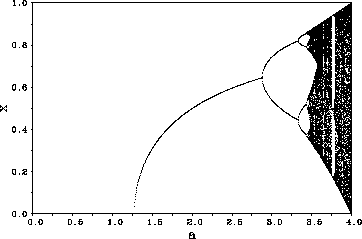
Figure: Bifurkationsszenario der Gleichung ( )
)
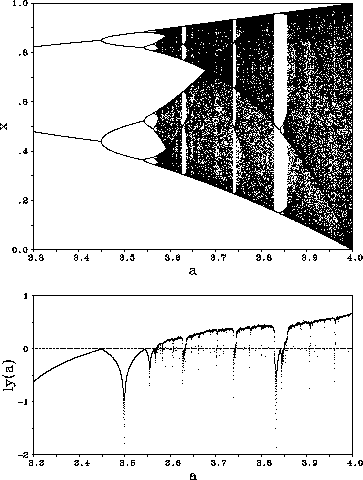
Figure: Ausschnittvergrößerungen der Abbildungen
 und
und 