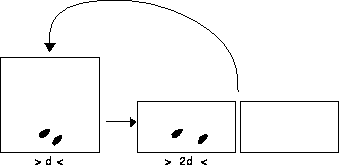
Figure: Prinzip der Bäcker-Transformation
Die Bäcker-Transformation
beschreibt ein zweidimensionales mathematisches Modell der Blätterteigproduktion (Die Schreibweise ,,mod 1`` bedeutet den gebrochenen Teil der Zahl): Ein Stück Teig wird in einem Knetzyklus auf die doppelte Länge ausgewalzt, in der Mitte auseinandergeschnitten und das rechte Stück auf das linke gelegt.
Hier läßt sich besonders gut die Sensitivität auf die Anfangsbedingung
zeigen: Wir betrachten dazu zwei dicht beieinanderliegende Rosinen
im Teig. Offensichtlich verdoppelt sich deren Abstand in x-Richtung
bei jedem Knetzyklus. Hatten die beiden Rosinen einen Anfangsabstand von
nur etwa einem Atomdurchmesser (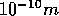
) so ist dieser nach
33 Knetzyklen auf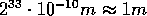 
angewachsen.
Damit ist klar, daß selbst die einfache Aussage, in welcher der beiden
Hälften des Teiges eine bestimmte Rosine nach 33 Knetzyklen liegen
wird, unmöglich ist.
In welcher Hälfte die Rosine nach n Knetzyklen liegt, hängt nämlich
genau von der n-ten Binärstelle (nach dem Komma) des Anfangswertes ab,
wenn man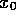 
als Binärbruch (alle 
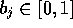) schreibt:
Die Multiplikation mit 2 ist in Binärdarstellung eine
Verschiebung
aller Stellen nach links (analog zu einer Multiplikation mit 10 in
Dezimaldarstellung). Die Operation ,,mod 1`` besteht im Nullsetzen
der Ziffern vor dem Komma.
