



Next: Kausalität
Up: Sensitivität auf Anfangsbedingungen
Previous: Bäcker-Transformation
Die Sensitivität auf kleine Änderungen der Anfangsbedingungen
kann quantifiziert werden. Bei der Bäckertransformation verdoppelt sich
eine Anfangsdifferenz  bei jedem Knetzyklus, sodaß die Differenz
nach n Zyklen zu
bei jedem Knetzyklus, sodaß die Differenz
nach n Zyklen zu
 ergibt.
Exponentielles Wachstum wird normalerweise zur Basis e definiert. Als die
für das exponentielle Anwachsen der Differenz bei der Bäckertransformation
charakteristische Zahl ergibt sich demnach
ergibt.
Exponentielles Wachstum wird normalerweise zur Basis e definiert. Als die
für das exponentielle Anwachsen der Differenz bei der Bäckertransformation
charakteristische Zahl ergibt sich demnach  .
Wir bezeichnen
.
Wir bezeichnen 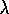 als Lyapunov-Exponenten.
Er ist der natürliche Logarithmus der
Streckungsrate
als Lyapunov-Exponenten.
Er ist der natürliche Logarithmus der
Streckungsrate 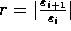 .
.
Für eindimensionale Abbildungen 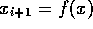 ,
für die die Streckungsrate r nicht konstant ist,
muß geeignet gemittelt werden, um ein globales Maß für die
Sensitivität auf Anfangsbedingungen zu gewinnen.
Wir betrachten eine Folge von Werten
,
für die die Streckungsrate r nicht konstant ist,
muß geeignet gemittelt werden, um ein globales Maß für die
Sensitivität auf Anfangsbedingungen zu gewinnen.
Wir betrachten eine Folge von Werten  und eine Folge von benachbarten
Werten
und eine Folge von benachbarten
Werten 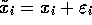 .
.
Der lokale Streckungsfaktor r ergibt sich als
Ableitung der Funktion  :
:

Der Lyapunovexponent ergibt sich nun als Mittel des natürlichen Logarithmuns
von r über eine lange Reihe von Werten  :
:

Für mehrdimensionale Abildungen oder kontinuierliche Modelle existieren
andere Definitionen der Lyapunov-Exponenten (vgl. [LL83,LKP87]). Dabei gibt
es pro Dimension einen Lyapunov-Exponenten.
Mithilfe des Lyapunovexponenten ist es möglich eine Definition für
chaotische Systeme anzugeben: Chaotische Systeme haben (mindestens)
einen positiven Lyapunov-Exponenten.
Diese Definition ist offensichtlich nicht sinnvoll für Systeme wie dem
Doppelpendel mit Reibung.
Hier ergeben sich negative Lyapunovexponenten, weil das
Langzeitverhalten regulär ist (Pendel verharrt in Ruhelage).
Trotzdem herrscht temporär Chaos, das eine mittelfristige Vorhersage
unmöglich macht. Dem kann man Rechnung tragen, wenn man eine andere
Art der Mittelung in ( ) wählt.
) wählt.
Vorhersagezeitraum bei chaotischen Systemen
Aus dem Spektrum der Lyapunov-Exponenten läßt sich ein Maß für die
maximale Dauer 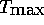 angeben,
über die eine Vorhersage sinnvoll ist berechnen [Far82]:
angeben,
über die eine Vorhersage sinnvoll ist berechnen [Far82]:

Dabei ist  die Unsicherheit in den Anfangsbedingungen, die
nur logarithmisch in
die Unsicherheit in den Anfangsbedingungen, die
nur logarithmisch in 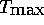 eingeht.
Eine Verbesserung der Meßgenauigkeit wirkt
sich also nur schwach auf den möglichen Vorhersagezeitraum aus.
Für Systeme mit ortsunabhängigen Lyapunov -Exponenten ergibt sich K
einfach als Summe der positiven Lyapunov -Exponenten:
eingeht.
Eine Verbesserung der Meßgenauigkeit wirkt
sich also nur schwach auf den möglichen Vorhersagezeitraum aus.
Für Systeme mit ortsunabhängigen Lyapunov -Exponenten ergibt sich K
einfach als Summe der positiven Lyapunov -Exponenten:





Next: Kausalität
Up: Sensitivität auf Anfangsbedingungen
Previous: Bäcker-Transformation
Werner Eberl
Sat Apr 15 13:17:50 MET DST 1995
 bei jedem Knetzyklus, sodaß die Differenz
nach n Zyklen zu
bei jedem Knetzyklus, sodaß die Differenz
nach n Zyklen zu
 ergibt.
Exponentielles Wachstum wird normalerweise zur Basis e definiert. Als die
für das exponentielle Anwachsen der Differenz bei der Bäckertransformation
charakteristische Zahl ergibt sich demnach
ergibt.
Exponentielles Wachstum wird normalerweise zur Basis e definiert. Als die
für das exponentielle Anwachsen der Differenz bei der Bäckertransformation
charakteristische Zahl ergibt sich demnach  .
Wir bezeichnen
.
Wir bezeichnen 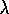 als Lyapunov-Exponenten.
Er ist der natürliche Logarithmus der
Streckungsrate
als Lyapunov-Exponenten.
Er ist der natürliche Logarithmus der
Streckungsrate 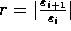 .
.




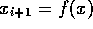 ,
für die die Streckungsrate r nicht konstant ist,
muß geeignet gemittelt werden, um ein globales Maß für die
Sensitivität auf Anfangsbedingungen zu gewinnen.
Wir betrachten eine Folge von Werten
,
für die die Streckungsrate r nicht konstant ist,
muß geeignet gemittelt werden, um ein globales Maß für die
Sensitivität auf Anfangsbedingungen zu gewinnen.
Wir betrachten eine Folge von Werten  und eine Folge von benachbarten
Werten
und eine Folge von benachbarten
Werten 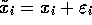 .
.
 :
:

 :
:


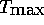 angeben,
über die eine Vorhersage sinnvoll ist berechnen [
angeben,
über die eine Vorhersage sinnvoll ist berechnen [
 die Unsicherheit in den Anfangsbedingungen, die
nur logarithmisch in
die Unsicherheit in den Anfangsbedingungen, die
nur logarithmisch in 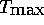 eingeht.
Eine Verbesserung der Meßgenauigkeit wirkt
sich also nur schwach auf den möglichen Vorhersagezeitraum aus.
eingeht.
Eine Verbesserung der Meßgenauigkeit wirkt
sich also nur schwach auf den möglichen Vorhersagezeitraum aus.
