



Next: Trajektorien
Up: Bunte Bilder in
Previous: Parameter-Landkarten
Ebenfalls technisch interessant sind Übersichtskarten, aus denen
hervorgeht, welche Anfagsbedingungen welches Verhalten erzeugen.
Für die Iterations-Abbildung, deren Parameterkarte das
sog. Apfelmännchen ergibt, lassen sich für festgelegte Werte
von 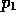 und
und 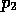 auch Anfangsbedingungs-Landkarten zeichnen.
Diese Mengen der Anfangswerte, für die die Iteration (
auch Anfangsbedingungs-Landkarten zeichnen.
Diese Mengen der Anfangswerte, für die die Iteration ( )
beschränkt bleibt, für die heißen Julia-Mengen.
)
beschränkt bleibt, für die heißen Julia-Mengen.
Interessanterweise sind die Julia-Mengen genau dann einfach zusammenhängend,
wenn die zugehörigen Parameterwerte innerhalb des Apfelmännchens liegen.
Die Mathematiker Julia und Fatou fanden dieses Resultat
anfang des 20. Jahrhunderts, ohne jemals
ein Apfelmännchen oder eine Julia-Menge grafisch gesehen zu haben!
Anwendungsbezogener ist aber wieder eine Darstellung für den
Helmholtz-Oszillator (Abb.  ).
).
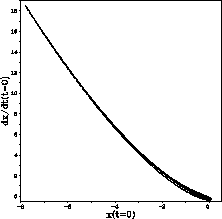
Figure: Einzugsbereich des seltsamen Attraktors beim Helmholtz-Oszillator
(schwarz) für 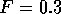 und
und 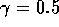 .
Die weiß gelassenen Gebiete gehören zum Einzugsbereich
des Attraktors bei
.
Die weiß gelassenen Gebiete gehören zum Einzugsbereich
des Attraktors bei 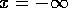 .
.
Werner Eberl
Sat Apr 15 13:17:50 MET DST 1995
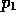 und
und 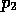 auch Anfangsbedingungs-Landkarten zeichnen.
Diese Mengen der Anfangswerte, für die die Iteration (
auch Anfangsbedingungs-Landkarten zeichnen.
Diese Mengen der Anfangswerte, für die die Iteration ( )
beschränkt bleibt, für die heißen Julia-Mengen.
)
beschränkt bleibt, für die heißen Julia-Mengen. 




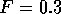 und
und 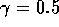 .
Die weiß gelassenen Gebiete gehören zum Einzugsbereich
des Attraktors bei
.
Die weiß gelassenen Gebiete gehören zum Einzugsbereich
des Attraktors bei 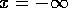 .
.