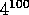 Funktionswerte
berechnen, was auf einer CRAY Y-MP etwa
Funktionswerte
berechnen, was auf einer CRAY Y-MP etwa 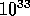 Jahre brauchen würde.
Jahre brauchen würde.




Der oben beschriebene Algorithmus ist eine neue Methode, mit der man in praxi das Problem der nichtlinearen Optimierung angehen kann, das theoretisch im allgemeinen nicht in endlicher Zeit auf einer Rechenanlage lösbar ist. Die nichtlineare Optimierung gehört zu den sog. NP-harten Problemen, d.h. die Komplexität des Algorithmus, die Anzahl der durchzuführenden Rechenoperationen wächst schneller als polynomial (Nicht Polynomial) mit der Komplexität des Problems.
Das heißt nicht, daß keines der NP-harten Probleme gelöst werden kann, es heißt nur, daß es keinen Algorithmus gibt, der alle NP-harten Probleme in endlicher Zeit lösen kann.
Das Problem bei der nichtlinearen Optimierung liegt darin, daß man nicht
jede Ecke des Definitionsgebietes untersuchen kann, weil es einfach
in einem hochdimensionalen Raum zuviele Ecken gibt. Wollte man sich
rein numerisch einen Überblick über den Verlauf einer Funktion mit
100 Variablen verschaffen, indem man pro Variable an 4 Stützstellen
den Funktionswert bestimmt, so müßte man 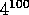 Funktionswerte
berechnen, was auf einer CRAY Y-MP etwa
Funktionswerte
berechnen, was auf einer CRAY Y-MP etwa 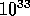 Jahre brauchen würde.
Jahre brauchen würde.
Die eine Strategie, um ohne die Beleuchtung jedes Winkels auszukommen, ist die Verwendung stochastischer Algorithmen (Simulated Annealing, genetische Algorithmen). Der oben beschriebene Bisektions-Algorithmus umgeht das Problem dadurch, daß analytisch berechnete Unter- und Ober-Grenzen es ermöglichen, ganze Teilintervalle von der weiteren Untersuchung auszuschließen. In jedem Teilschritt werden nur absolut sichere Aussagen erzielt.
Die Rechenzeit wächst im allgemeinen bei weiterer Verfeinerung des Gitters kaum an, da die Zahl der zu untersuchenden Teilintervalle ungefähr konstant bleibt. Das Anwachsen ist auf die länger werdenden rationalen Zahlen zurückzuführen, die durch ihre ,,unendliche Genauigkeit`` numerische Probleme ausschließen.
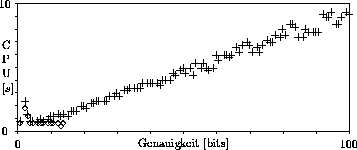
Figure: Rechenzeit pro Iteration des Algorithmus bei der Suche des Maximums
von 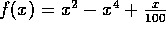 im Intervall
im Intervall
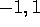 auf einer DEC RISC workstation unter MATHEMATICA 1.2
als Funktion der erreichten Genauigkeit.
+: Verwendung von rationalen Zahlen,
auf einer DEC RISC workstation unter MATHEMATICA 1.2
als Funktion der erreichten Genauigkeit.
+: Verwendung von rationalen Zahlen,
 : Verwendung von Fließkommazahlen (32 bit)
: Verwendung von Fließkommazahlen (32 bit)
Während der ersten Iterationen können normalerweise nicht alle Intervalle bis auf eines eliminiert werden. Dadurch wächst die benötigte Rechenzeit pro Iteration zunächst an. Jedoch verbessert sich die Güte der Abschätzungen, wenn die Intervalle kleiner werden, sodaß in den folgenden Iterationen die Zahl der Intervall-Kandidaten wieder drastisch sinkt.
Bei Verwendung von rationaler (exakter) Arithmetik
steigt die Rechenzeit etwa linear mit der Zahl der benötigten Ziffern zur
Darstellung der Intervallgrenzen (vgl. Bild  ).
).



