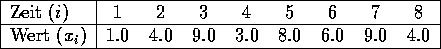
Gegeben sei eine Zeitreihe von N=8 Meßdaten:
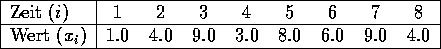
Um die Anschaulichkeit zu erhöhen, stelle man sich vor, es handle sich um Monatsanfangskurse einer Aktie. Die Daten könnten genausogut aufeinanderfolgende Punkte eines Poincaré-Schnitts oder irgendwelche anderen Daten sein, deren Dynamik modelliert werden soll.
Wir nehmen nun an, daß der nächste Wert der Reihe wenigstens
näherungsweise aus dem vorhergehenden durch eine Funktion
bestimmt ist: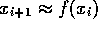 
. Um die Funktion zu ermitteln
tragen wir zunächst die Daten in ein Diagramm ein (linkes Bild in
Abb. 
).
Figure: links: Next-x-Abbildung der Beispiel-Zeitreihe. rechts:
Derselbe Plot, aber zusätzlich mit der an die Punkte optimal
angepaßten quadratischen Parabel
Offensichtlich liegen die Punkte nicht auf einer
Geraden. Die nächsteinfache Kurve ist eine quadratische Parabel
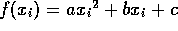, deren Parameter a,b,c wir nun so bestimmen
wollen, daß die mittlere quadratische Abweichung Q der mit dieser Funktion
vorhergesagten Werte von den tatsächlich eingetretenen minimal wird:
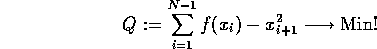
Die Summe ergibt in unserem Beispiel:
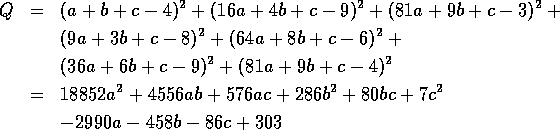
Q hängt offensichtlich jetzt nur noch von den drei Modellparametern
a,b,c ab, die dadurch zu bestimmen sind, daß man die Stelle des Minimums
von Q sucht. Im vorliegenden Fall kann man dies durch Lösen des
Gleichungssystems
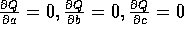bewerkstelligen und erhält:
, 
, 
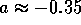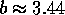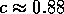
Damit könnte man den nächsten Wert der Zeitreihe vorhersagen:
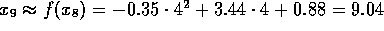
Mit diesen einfachen Methoden kann man noch nichts über Vertrauensintervalle für die Modellparameter oder die Vorhersagen aussagen. Dazu bräuchte man eine nichtlineare Regressionsanalyse. Damit könnte auch geklärt werden, ob es sinnvoll ist, statt der quadratischen Parabel eine kubische oder eine mit noch höheren Termen anzusetzen.