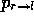 für eine Kugel, dieses zu tun, multipliziert mit der Zahl
für eine Kugel, dieses zu tun, multipliziert mit der Zahl 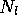 der links liegenden Kugeln. Ist die Apparatur symmetrisch gebaut,
muß gelten:
der links liegenden Kugeln. Ist die Apparatur symmetrisch gebaut,
muß gelten: 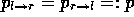




Eine Kugel, die genügend hoch hüpft, landet mit gleicher
Wahrscheinlichkeit auf beiden Seiten der Trennwand. Hüpft die
Kugel nicht so hoch, ist die Wahrscheinlichkeit größer, daß
sie auf der gleichen Hälfte bleibt. Die Zahl der Teilchen, die
pro Zeitintervall dt von links nach rechts hüpfen,
ist das Produkt aus der Wahrscheinlichkeit 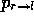 für eine Kugel, dieses zu tun, multipliziert mit der Zahl
für eine Kugel, dieses zu tun, multipliziert mit der Zahl 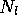 der links liegenden Kugeln. Ist die Apparatur symmetrisch gebaut,
muß gelten:
der links liegenden Kugeln. Ist die Apparatur symmetrisch gebaut,
muß gelten: 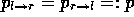
Es läßt sich nun eine Bilanz-Gleichung aufschreiben:
Fall I: p=const.
Diese Differentialgleichung ist linear und hat genau einen Wert für
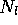 bzw.
bzw. 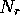 , für den die zeitlichen Ableitungen verschwinden,
sich also ein stationärer Wert einstellt:
, für den die zeitlichen Ableitungen verschwinden,
sich also ein stationärer Wert einstellt: 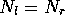 .
Dieser Fixpunkt der Differentialgleichung ist auch stabil, d.h.
kleine Abweichungen von der Gleichverteilung verschwinden wieder.
.
Dieser Fixpunkt der Differentialgleichung ist auch stabil, d.h.
kleine Abweichungen von der Gleichverteilung verschwinden wieder.
Fall II: 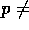 const.
const.
Tatsächlich hängt aber p von der Zahl der Kugeln ab, die bereits
auf einer Seite liegen. Liegen bereits viele Kugeln auf einer Seite,
dann werden die Stöße viel stärker gedämpft, und die
Wahrscheinlichkeit für einen Wechsel auf die andere Seite sinkt.
Ist die Nichtlinearität genügend groß, wird der Fixpunkt 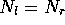 instabil. Kleine Abweichungen von der Gleichverteilung verstärken sich
dann immer weiter. Die Gleichung hat nun zwei neue, zusätzliche
Fixpunkte, die beide stabil sind. Welcher von beiden erreicht
wird, hängt von der exakten Anfangsbedingung ab.
instabil. Kleine Abweichungen von der Gleichverteilung verstärken sich
dann immer weiter. Die Gleichung hat nun zwei neue, zusätzliche
Fixpunkte, die beide stabil sind. Welcher von beiden erreicht
wird, hängt von der exakten Anfangsbedingung ab.
LEITFÄHIGE TEILCHEN IM ELEKTRISCHEN FELD