Ziele der Modellbildung für dynamische Prozesse

. ZIELE DER MODELLBILDUNG Von einem guten Modell wird vor allem erwartet:

• Einfachheit:€Das Modell soll wesentlich weniger Daten enthalten als die Zeitreihe.
• Vorhersage: Der weitere Verlauf einer Zeitreihe soll aus dem bisherigen vorhergesagt werden können. Für chaotische Systeme muß man sich auf Kurzzeitvorhersagen beschränken, während für reguläre Systeme Langzeitvorhersagen interessant sind.
• Reproduzierbarkeit: verschiedene Läufe des Experiments sollen zu den gleichen Modellparametern führen. Bei chaotischen Systemen ist die konkrete Zeitreihe nicht reproduzierbar, das Modell dazu soll es natürlich sehrwohl sein, da es sich ja bei jedem Lauf um das gleiche System handelt.
• Stetigkeit: kleine Änderungen physikalischer Parameter sollen nur kleine Änderungen an den Modellparametern hervorrufen.
• Steuerung: die Kenntnis eines guten Modells soll eine effektive Steuerung des Systems ermöglichen.
• Abschätzung verborgener Systemgrößen: Ist die Existenz einiger Größen zwar bekannt, aber deren Messung unmöglich, sollte ein gutes Modell zur Rekonstruktion der Dynamik der verborgenen Variablen führen.

 
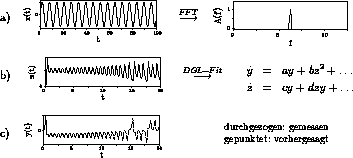
Figure: Ziele der Modellbildung: Aus gegebenen Zeitreihen sollen Modelle rekonstruiert werden, die mit wenigen, zeitlich konstanten Parametern auskommen. Bei periodischen Signalen (a) reduziert sich die Datenmenge der Zeitreihe auf die Angabe von Lage und Höhe der Peaks im Fourier-Spektrum. Im chaotischen Fall (b) ist eine Fourier-Transformation sinnlos, weil die Zahl der notwendigen Komponenten ungefähr der Zahl der Datenpunkte entspricht, weshalb man hier besser nichtlineare Differentialgleichungen an die experimentelle Dynamik anpaßt. Die Modelle sollen auch --- wenigstens kurzzeitige --- Vorhersagen ermöglichen (Teilbild c).

Als Modelle für Zeitreihen erscheinen deshalb vor allem diskrete Abbildungen und gewöhnliche Differentialgleichungen geeignet, während für Systeme mit vielen Freiheitsgraden partielle Differentialgleichungen oder zelluläre Automaten sinnvoll sind.

In der Chaosforschung macht man nun einige grundlegende Annahmen bei der Modellbildung für Zeitreihen:

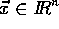• Das System wird zu jedem Zeitpunkt durch seinen Zustand charakterisiert.
• Die Dynamik des Systems ist die zeitliche Folge der Zustände
• es existiert eine weitgehend deterministische Regel für
  • die Richtung der momentanen Zustandsänderung oder
  • den neuen Zustand zu einer späteren Zeit als Funktion des aktuellen Zustands

Die komplexe Dynamik wird modelliert mit einem möglichst niederdimensionalen (n<10) deterministischen Modell und einem Rauschterm. Das Modell wird dadurch einfacher, weil man nur verlangen muß, daß es innerhalb der Rauschbreite korrekte Aussagen liefert. Für einige Zwecke kann der Rauschanteil relativ groß gewählt werden (Beispiel: Steuerung, vgl Kapitel ).