Für kleine Zeitschritte 
läßt sich die Differentialgleichung
(6.1)
mit Hilfe eines Euler-Schritts in eine stroboskopische Abbildung umformen.
Der Ansatz bis zu den wichtigen Moden (vgl. Abschnitt 2.2.4)
führt für 
auf 
, 
,
, 
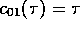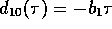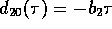und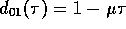 
.
ist hier das Meß- und Steuerintervall (20 ms) und damit
klein im Vergleich zur Schwingungsdauer des Rades
(>2s).
Mit einem Least-Square-Fit gemäß Abschnitt 4.1.1
wurden ungefähre Werte für die Parameter 
, 
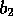und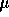 
bestimmt.
Zur Bestimmung von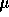 
wurde dazu der in Abschnitt 4.1.2
erwähnte Trick zur verbesserten Bestimmung der vom Langzeitverhalten bestimmten
Parameter verwendet:
Zuerst verschafft man sich die exakten Ausdrücke für die fünf wichtigen Koeffizienten gemäß Abschnitt 2.2.4:
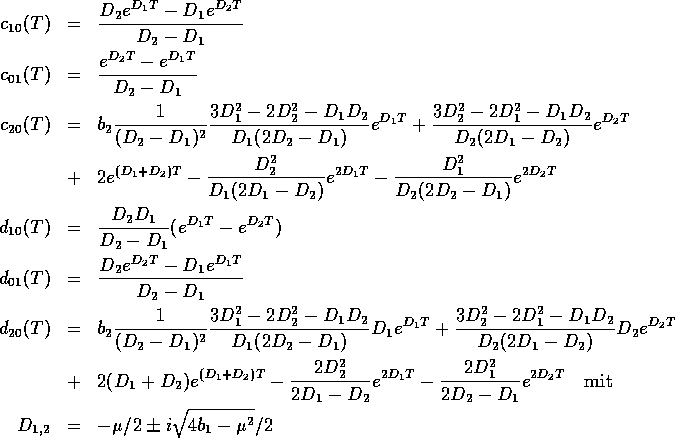
Damit ist eine Relation zwischen den Koeffizienten für verschiedene
T gegeben. So läßt sich der Koeffizient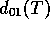 
für Werte von T durch Fit ermitteln, die etwa ein Viertel der
Schwingungsperiode des Systems betragen und damit das Dämpfungsverhalten
wesentlich präziser widerspiegeln als kleine Zeitschritte.
Den für die Steuerung brauchbaren Wert 
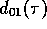kann man nun aus den
obigen Formeln ermitteln.
