Gegeben sei ein experimentelles System, dessen Dynamik durch eine
Abbildung 
beschrieben werden kann:
Dabei sei 
der
Zustandsvektor des Systems zum Zeitpunkt
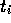und 
die --- noch zu berechnende --- Steuerkraft, die bei
appliziert werden soll. Falls 
eine stroboskopische Abbildung
ist, gilt: 
, wobei T die Stroboskopierzeit ist.
Im Falle von Poincaré
-Abbildungen sind die 
durch die Zeitpunkte des
Durchstoßes der Trajektorie durch die Poincaré
-Ebene gegeben.
Von der Eigendynamik des experimentellen Systems existiere ein Modell:
Dieses Modell soll nicht zu schlecht sein, d.h. es soll gelten:
. Zunächst soll der Einfachheit halber
nur der Fall 
und 
behandelt werden; das Modell soll exakt sein.
Die Auswirkungen von Abweichungen in den Modellparametern
wird in [CHP89] diskutiert und im Abschnitt
5.4 zur genauen Ermittlung der Modellparameter
verwendet.
Die Wunschdynamik kann man ebenfalls als Abbildung definieren:
Die Abweichung 
der Istdynamik von der
Solldynamik muß für 
gegen Null streben, wenn die Steuerung
stabil sein soll.
Die Wahl
für die Antriebskraft bewirkt offensichtlich eine Zerstörung
der Eigendynamik des Systems und eine Etablierung der Wunschdynamik.
wird dadurch bereits nach dem ersten Schritt exakt Null.
In diese Steuerkraft geht aber noch 
ein, es ist
also Rückkopplung notwendig.
Der rückkopplungsfreie Ansatz
führt zu einem gesteuerten System, dessen Abweichung folgender Iterationsgleichung gehorcht:
ist dabei offensichtlich ein Fixpunkt der Funktion
, d.h. wenn das System einmal den Wunschzustand erreicht,
wird es ihn auch beibehalten. Interessanter ist aber die Frage nach der
Stabilität dieses Fixpunktes, also die Frage, ob eine erfolgreiche
Steuerung auch dann möglich ist, wenn der Anfangszustand des experimentellen
Systems unbekannt ist oder Rauschen vorliegt.
Lineare Stabilitätsanalyse liefert folgende hinreichende Bedingung
für die Stabilität der Steuerung
:
