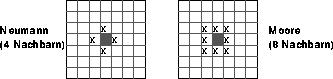
Figure: Nachbarschaftsdefinitionen beim quadratischen Gitter
Als Gittergeometrie verwendet man im allgemeinen quadratische oder hexagonale Gitter. Für das zweidimensionale, quadratische Gitter gibt es zwei gebräuchliche Nachbarschaftsdefinitionen: Die von Neumann-Nachbarschaft besteht nur aus den 4 nächsten Nachbarn, während die Moore-Nachbarschaft auch die 4 diagonalen Nachbarn miteinbezieht.
Mathematisch schreibt sich ein von Neumann-Zellularautomat wie folgt:
Dabei sind die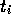 
diskrete Zeitpunkte. Die Indizes j und k
bezeichnen den Ort der Zelle.
Statt quadratischen Gittern verwendet man gerne auch hexagonale oder
trigonale Gitter. Entscheidend ist, daß bei deterministischen,
synchronen Automaten auf regelmäßigen Gittern sich die Geometrie
des Gitters auf die Geometrie der Lösung überträgt, unabhängig
von der Gitterweite. Man beachte das Beispiel in Abb. 
,
wo rechteckige Spiralen entstehen. Auf einem hexagonalen Gitter
würden hexagonale Spiralen entstehen.
