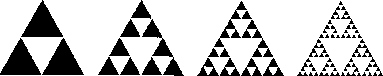
Figure: Die ersten vier Schritte, die zum Sierpinski-Dreieck führen, einem deterministisches Fraktal




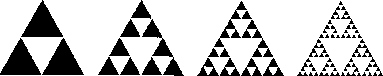
Figure: Die ersten vier Schritte, die zum Sierpinski-Dreieck führen, einem
deterministisches Fraktal
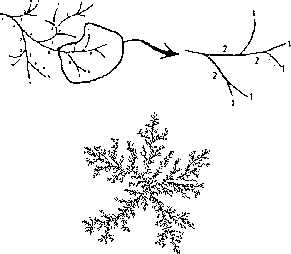
Figure: Beispiele für statistische Fraktale
Eine makroskopische Beschreibungsgröße für komplexe räumliche
Strukturen ist die sogenannte
fraktale Dimension. Ein mathematisches (= deterministisches)
Fraktal ist ein geometrisches Objekt, das durch iterative Anwendung einer
mathematischen Abbildung entsteht (siehe Abb.  ).
Es besitzt
die Eigenschaft der Selbstähnlichkeit. Salopp gesprochen heißt das,
daß ein irgendwo herausgeschnittenes Stück nach Vergrößerung genauso
aussieht wie das ursprüngliche Fraktal. Es gibt aber auch geometrische
Objekte, die nur in einem statistischen Sinne fraktal sind. Dazu können
Dendriten gehören. Bei ihnen hat ein herausgeschnittenes und
anschließend vergrößertes Stück nur im Mittel dieselbe
Auftretenswahrscheinlichkeit wie das Gesamtobjekt (siehe Abbildung
).
Es besitzt
die Eigenschaft der Selbstähnlichkeit. Salopp gesprochen heißt das,
daß ein irgendwo herausgeschnittenes Stück nach Vergrößerung genauso
aussieht wie das ursprüngliche Fraktal. Es gibt aber auch geometrische
Objekte, die nur in einem statistischen Sinne fraktal sind. Dazu können
Dendriten gehören. Bei ihnen hat ein herausgeschnittenes und
anschließend vergrößertes Stück nur im Mittel dieselbe
Auftretenswahrscheinlichkeit wie das Gesamtobjekt (siehe Abbildung
 ). Solche Gebilde bezeichnet man als skaleninvariant.
Analog zu einem Würfel, dessen Masse mit seiner linearen
Ausdehnung in der Potenz seiner Dimension (hier also
). Solche Gebilde bezeichnet man als skaleninvariant.
Analog zu einem Würfel, dessen Masse mit seiner linearen
Ausdehnung in der Potenz seiner Dimension (hier also 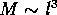 )
skaliert, läßt sich für selbstähnliche oder skaleninvariante
Objekte eine - in der Regel allerdings gebrochenzahlige (=fraktale) -
Dimension definieren, die das Massenskalierugsverhalten beschreibt.
Bei dem in Abbildung
)
skaliert, läßt sich für selbstähnliche oder skaleninvariante
Objekte eine - in der Regel allerdings gebrochenzahlige (=fraktale) -
Dimension definieren, die das Massenskalierugsverhalten beschreibt.
Bei dem in Abbildung  gezeigten Objekt kommt man über
die entsprechende mathematische Abbildungsvorschrift zu einem
Skalierugsverhalten
gezeigten Objekt kommt man über
die entsprechende mathematische Abbildungsvorschrift zu einem
Skalierugsverhalten 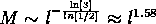 .
Bei statistischen Fraktalen bestimmt man die
fraktale Dimension durch Bestimmung der Masse für jeweils verschiedene
Längenskalen l, beispielsweise mit einem Boxcounting-Algorithmus,
bei dem das geometrische Objekt
mit einem Raster variierender Kantenlänge belegt wird
(siehe Abbildung
.
Bei statistischen Fraktalen bestimmt man die
fraktale Dimension durch Bestimmung der Masse für jeweils verschiedene
Längenskalen l, beispielsweise mit einem Boxcounting-Algorithmus,
bei dem das geometrische Objekt
mit einem Raster variierender Kantenlänge belegt wird
(siehe Abbildung  ). Es wird dann jeweils
gezählt, wieviele Rasterkästchen einen Teil der Figur enthalten,
um daraus nach
). Es wird dann jeweils
gezählt, wieviele Rasterkästchen einen Teil der Figur enthalten,
um daraus nach
und ,,Anfitten`` der Steigung die fraktale Dimension D zu bestimmen.
Es gibt eine Vielzahl teils sehr verschieden definierter fraktaler Dimensionen, für die stellvertretend hier die wohl am einfachsten bestimmbare Boxcounting-Dimension (der Einfachheit halber nur als fraktale Dimension bezeichnet) aufgeführt wird. Mit ihr läßt sich eine experimentell erzeugte dendritische Struktur --- wie sie bespielsweise bei dem eben beschriebenen Kügelchenexperiment erzeugt wird --- nach einer photographischen Aufnahme und anschließendem Einlesen der Positionen in den Computer problemlos geometrisch mit gleichartigen Strukturen vergleichen.
Historisch gesehen entstand der Begriff der fraktalen Dimension
im Zusammenhang mit der Frage, wie lange die Küstenlinie Englands sei.
Richardson widmete sich diesem Problem und stellte fest, daß
die gemessene Länge der Küste (= Länge eines Maßstabs 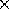 Zahl der
angelegten Maßstäbe) immer weiter zunimmt, je kleiner man den Maßstab
wählt. Dies ist leicht dadurch zu erklären, daß man mit einem
immer kleineren Maßstab immer kleinere Buchten erfassen kann.
Zahl der
angelegten Maßstäbe) immer weiter zunimmt, je kleiner man den Maßstab
wählt. Dies ist leicht dadurch zu erklären, daß man mit einem
immer kleineren Maßstab immer kleinere Buchten erfassen kann.
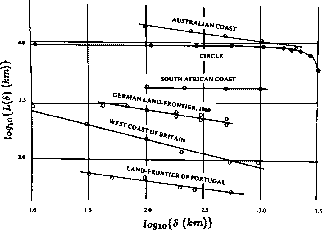
Figure: Auftragung der Messungen von Küstenlinien aufgrund der
Daten, die Richardson vorlagen. Man beachte, daß die negative Steigung
der Geraden hier nicht die fraktale Dimension ist, weil auf der
Ordinate nicht die Zahl der Maßstäbe, sondern die gemessene Länge
aufgetragen ist. Die fraktale Dimension ist genau um 1 höher.



