 . PRÄDIKTION EINER FUNKTION DURCH EIN N.N.
. PRÄDIKTION EINER FUNKTION DURCH EIN N.N.




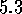 . PRÄDIKTION EINER FUNKTION DURCH EIN N.N.
. PRÄDIKTION EINER FUNKTION DURCH EIN N.N.
Nachdem das Netz ,,ausgelernt`` hat, wird es mit Eingaben getestet, die nicht unter den Trainingsmustern waren. Dabei kann das Netz sowohl Interpolation als auch Extrapolation durchführen:
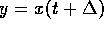 für ein
für ein 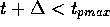 zu berechnen ist, und
zu berechnen ist, und
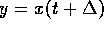 für ein
für ein
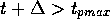 zu bestimmen ist.
zu bestimmen ist.
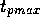 den größten Wert von
den größten Wert von 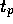 , der in den
Trainingsmustern aufgetreten ist.
, der in den
Trainingsmustern aufgetreten ist.
Um eine Aussage über die Qualität der Vorhersage des neuronalen
Netzes machen zu können, empfiehlt es sich, ein Maß 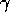 für die
Genauigkeit der Vorhersage einzuführen. Für q vom Netzwerk
vorhergesagte Punkte berechnet sich
für die
Genauigkeit der Vorhersage einzuführen. Für q vom Netzwerk
vorhergesagte Punkte berechnet sich 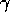 durch
durch
wobei
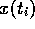 der tatsächliche Funktionswert zum Zeitpunkt
der tatsächliche Funktionswert zum Zeitpunkt 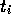 ,
,
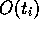 die Vorhersage des Netzes für den Funktionswert
zum Zeitpunkt
die Vorhersage des Netzes für den Funktionswert
zum Zeitpunkt 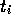 , und
, und
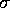 die Standardabweichung der vorhergesagten Punkte ist.
die Standardabweichung der vorhergesagten Punkte ist.
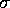 bewirkt, daß
bewirkt, daß 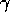 unabhängig vom
gewählten Maßstab wird, wodurch ein objektiver Vergleich
der Qualität verschiedener
Vorhersagen der Funktion möglich wird.
unabhängig vom
gewählten Maßstab wird, wodurch ein objektiver Vergleich
der Qualität verschiedener
Vorhersagen der Funktion möglich wird.
Wie aus den Gleichungen ( ) und
(
) und
( ) zu ersehen ist, wird ein neuronales Netz
immer nur für genau ein
) zu ersehen ist, wird ein neuronales Netz
immer nur für genau ein 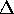 trainiert. D. h., ein
einziges Netz kann eine Funktion nur für
trainiert. D. h., ein
einziges Netz kann eine Funktion nur für 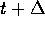 vorhersagen. Möchte man aber Vorhersagen für verschiedene
vorhersagen. Möchte man aber Vorhersagen für verschiedene
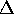 haben, so muß man für jedes
haben, so muß man für jedes 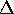 ein eigenes
Netzwerk nach dem obigen Verfahren trainieren. Steht jedoch nur
ein Netzwerk zur Verfügung, bietet sich folgende Lösung des Problems an:
ein eigenes
Netzwerk nach dem obigen Verfahren trainieren. Steht jedoch nur
ein Netzwerk zur Verfügung, bietet sich folgende Lösung des Problems an:
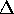 sehr klein. Dadurch liefert das trainierte
Netz sehr genaue Vorhersagen des Funktionswertes für
sehr klein. Dadurch liefert das trainierte
Netz sehr genaue Vorhersagen des Funktionswertes für 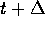 .
.
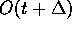 nach
(
nach
( ):
):
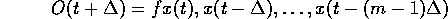
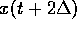 erhält man durch
erhält man durch
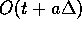 für
große a ein größerer Fehler auf, als es bei einem auf den Zeitraum
für
große a ein größerer Fehler auf, als es bei einem auf den Zeitraum
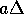 trainierten Netz der Fall sein würde. Für kleine
trainierten Netz der Fall sein würde. Für kleine 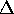 bleibt jedoch der Fehler auch für große a so gering, daß diese
Art der Vorhersage von Funktionswerten auf Grund ihrer größeren
Variabilität durchaus zu bevorzugen ist.
bleibt jedoch der Fehler auch für große a so gering, daß diese
Art der Vorhersage von Funktionswerten auf Grund ihrer größeren
Variabilität durchaus zu bevorzugen ist.



