



Next: Suche des absoluten
Up: Verfahren zur nichtlinearen
Previous: Nichtlineare Optimierung als
Der Begriff ,,Simulated Annealing`` steht für ein aus der Natur
abgeschautes Verfahren, um globale Minima oder Maxima einer Funktion zu
finden. Während andere Verfahren zum großen Teil in lokalen Minima
,,hängen`` bleiben können, ist es eine besondere Stärke des Algorithmus
aus diesen wieder herauszufinden. Die am Ende gefundene Lösung stellt
bei unendlicher Abkühlzeit mit Sicherheit das globale Minimum oder Maximum
dar, während dies bei endlicher Abkühlzeit nicht immer der Fall ist.
Beim langsamen Abkühlen eines Metallstückes ordnen sich die einzelnen
Atome so an, daß sie einen Zustand möglichst niedriger Energie einnehmen.
Tritt allerdings eine zu schnelle Abkühlung auf, so haben die Atome nicht
die Zeit das tatsächliche Minimum zu finden, das System bleibt in einem
lokalen Minimum ,,hängen``. Ein niedriger Energiezustand ist in diesem
Fall gleichbedeutend mit einem stabilen Endzustand, also einem sehr
stabilen Werkstück.
Diese Grundidee hat man nun verwendet, um bei mathematischen Funktionen
das Minimum oder äquivalent das Maximum (dazu nehme man das negative der
Funktion) zu finden. Sei eine Funktion 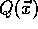 gegeben. Analog zu einem
Teilchen in einem Werkstück betrachtet man einen Vektor
gegeben. Analog zu einem
Teilchen in einem Werkstück betrachtet man einen Vektor 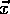 , dessen
Komponenten anfangs zufällig im jeweiligen Intervall bestimmt werden. Nun
wird eine zufällige Verschiebung
, dessen
Komponenten anfangs zufällig im jeweiligen Intervall bestimmt werden. Nun
wird eine zufällige Verschiebung 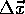 ausgelost; ist der neue
Funktionswert
ausgelost; ist der neue
Funktionswert 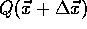 kleiner als der alte
kleiner als der alte 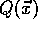 ,
so wird die neue Position verwendet. Diese Vorschrift stellt bereits einen
vollständigen Algorithmus zur Suche nach einem Minimum dar; allerdings mit
dem gravierenden Nachteil, daß der Algorithmus sich aus einem lokalen
Minimum nicht mehr befreien kann. Es geht stets nur zu niedrigeren
Funktionswerten. Um dieses Problem zu lösen ist beim Simulated Annealing
auch ein Sprung zu höheren Funktionswerten möglich. Dieser wird aber nur
mit einer bestimmten Wahrscheinlichkeit p ausgeführt. Diese berechnet
sich nach folgender Formel:
,
so wird die neue Position verwendet. Diese Vorschrift stellt bereits einen
vollständigen Algorithmus zur Suche nach einem Minimum dar; allerdings mit
dem gravierenden Nachteil, daß der Algorithmus sich aus einem lokalen
Minimum nicht mehr befreien kann. Es geht stets nur zu niedrigeren
Funktionswerten. Um dieses Problem zu lösen ist beim Simulated Annealing
auch ein Sprung zu höheren Funktionswerten möglich. Dieser wird aber nur
mit einer bestimmten Wahrscheinlichkeit p ausgeführt. Diese berechnet
sich nach folgender Formel:
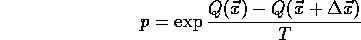
Der Kontroll-Parameter T stellt dabei das Analogon zur Temperatur T bei
einem Werkstück dar. Für hohe T-Werte ist p nahezu 1, d.h. fast jede
Verschiebung von 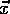 wird ausgeführt. Läßt man T nun gegen 0 gehen,
so wird die Wahrscheinlichkeit für einen Sprung auf ein höheres Niveau
immer geringer, wobei auch die Differenz
wird ausgeführt. Läßt man T nun gegen 0 gehen,
so wird die Wahrscheinlichkeit für einen Sprung auf ein höheres Niveau
immer geringer, wobei auch die Differenz 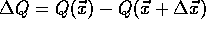 eine Rolle spielt. Für kleine Werte von
eine Rolle spielt. Für kleine Werte von 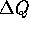 ist p
wiederum fast 1,
ist p
wiederum fast 1, 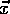 kann also in seiner näheren Umgebung (im Fall
stetiger Funktionen) noch frei verändert werden, dagegen für große
Werte von
kann also in seiner näheren Umgebung (im Fall
stetiger Funktionen) noch frei verändert werden, dagegen für große
Werte von 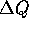 ist ein Sprung zwar möglich, aber sehr
unwahrscheinlich.
ist ein Sprung zwar möglich, aber sehr
unwahrscheinlich.
Mathematisch ist es bewiesen [VLAu87] daß das System für den Fall
unendlich kleiner Temperaturänderungen immer das globale Minimum findet.
In der Praxis möchte man jedoch meist nach endlicher Zeit ein Ergebnis
sehen, so daß man die Temperatur in größeren Schritten heruntersetzen
muß. Wann man nun die Temperatur weiter heruntersetzt und wann man noch
wartet, ist das eigentliche Problem. Es gibt im Prinzip zwei Ansätze:
- Man kühlt mit einer konstante Rate,
z.B.
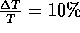 und wartet
dann, bis sich das System erneut eingeschwungen hat (Also das thermische
Gleichgewicht wieder hergestellt ist). Dies wird über statistische
Größen kontrolliert (man verwendet daher nicht nur einen Vektor
und wartet
dann, bis sich das System erneut eingeschwungen hat (Also das thermische
Gleichgewicht wieder hergestellt ist). Dies wird über statistische
Größen kontrolliert (man verwendet daher nicht nur einen Vektor 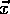 ,
sondern mehrere, z.B. 1000).
,
sondern mehrere, z.B. 1000).
- Man verwendet eine variable Kühlrate. Auch in diesem Fall finden
statistische Größen Verwendung, allerdings braucht man dazu
detailliertere Kenntnisse über das betrachtete System, um das System nicht
zu schnell abzukühlen, was dazu führen kann, daß das System sich in
einem lokalen Minimum verfängt.
Der Algorithmus läßt sich dann so schreiben:

,5cm
Eine bedeutende Anwendungsmöglichkeit dieses Verfahrens ist das sogenannte
TSP (Traveling Salesman Problem): Ein Handlungsreisender soll n
Städte bereisen und dabei den kürzesten Weg finden.
Bei diesem Problem gibt es ausgeprägte Nebenmaxima, weshalb andere
Algorithmen häufig versagen. Simulated Annealing findet zwar auch hier nicht
immer das globale Minimum, jedoch liegen die erreichten Werte meist nur
unwesentlich (1-10%) über dem Idealwert und sind damit für die Praxis
oft völlig ausreichend.




Next: Suche des absoluten
Up: Verfahren zur nichtlinearen
Previous: Nichtlineare Optimierung als
Werner Eberl
Sat Apr 15 13:17:50 MET DST 1995
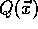 gegeben. Analog zu einem
Teilchen in einem Werkstück betrachtet man einen Vektor
gegeben. Analog zu einem
Teilchen in einem Werkstück betrachtet man einen Vektor 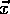 , dessen
Komponenten anfangs zufällig im jeweiligen Intervall bestimmt werden. Nun
wird eine zufällige Verschiebung
, dessen
Komponenten anfangs zufällig im jeweiligen Intervall bestimmt werden. Nun
wird eine zufällige Verschiebung 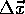 ausgelost; ist der neue
Funktionswert
ausgelost; ist der neue
Funktionswert 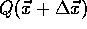 kleiner als der alte
kleiner als der alte 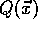 ,
so wird die neue Position verwendet. Diese Vorschrift stellt bereits einen
vollständigen Algorithmus zur Suche nach einem Minimum dar; allerdings mit
dem gravierenden Nachteil, daß der Algorithmus sich aus einem lokalen
Minimum nicht mehr befreien kann. Es geht stets nur zu niedrigeren
Funktionswerten. Um dieses Problem zu lösen ist beim Simulated Annealing
auch ein Sprung zu höheren Funktionswerten möglich. Dieser wird aber nur
mit einer bestimmten Wahrscheinlichkeit p ausgeführt. Diese berechnet
sich nach folgender Formel:
,
so wird die neue Position verwendet. Diese Vorschrift stellt bereits einen
vollständigen Algorithmus zur Suche nach einem Minimum dar; allerdings mit
dem gravierenden Nachteil, daß der Algorithmus sich aus einem lokalen
Minimum nicht mehr befreien kann. Es geht stets nur zu niedrigeren
Funktionswerten. Um dieses Problem zu lösen ist beim Simulated Annealing
auch ein Sprung zu höheren Funktionswerten möglich. Dieser wird aber nur
mit einer bestimmten Wahrscheinlichkeit p ausgeführt. Diese berechnet
sich nach folgender Formel:




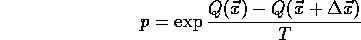
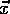 wird ausgeführt. Läßt man T nun gegen 0 gehen,
so wird die Wahrscheinlichkeit für einen Sprung auf ein höheres Niveau
immer geringer, wobei auch die Differenz
wird ausgeführt. Läßt man T nun gegen 0 gehen,
so wird die Wahrscheinlichkeit für einen Sprung auf ein höheres Niveau
immer geringer, wobei auch die Differenz 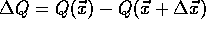 eine Rolle spielt. Für kleine Werte von
eine Rolle spielt. Für kleine Werte von 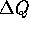 ist p
wiederum fast 1,
ist p
wiederum fast 1, 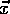 kann also in seiner näheren Umgebung (im Fall
stetiger Funktionen) noch frei verändert werden, dagegen für große
Werte von
kann also in seiner näheren Umgebung (im Fall
stetiger Funktionen) noch frei verändert werden, dagegen für große
Werte von 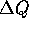 ist ein Sprung zwar möglich, aber sehr
unwahrscheinlich.
ist ein Sprung zwar möglich, aber sehr
unwahrscheinlich.
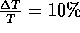 und wartet
dann, bis sich das System erneut eingeschwungen hat (Also das thermische
Gleichgewicht wieder hergestellt ist). Dies wird über statistische
Größen kontrolliert (man verwendet daher nicht nur einen Vektor
und wartet
dann, bis sich das System erneut eingeschwungen hat (Also das thermische
Gleichgewicht wieder hergestellt ist). Dies wird über statistische
Größen kontrolliert (man verwendet daher nicht nur einen Vektor 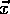 ,
sondern mehrere, z.B. 1000).
,
sondern mehrere, z.B. 1000).
