
"Ich kann den Computer doch gar nicht verstehen; er besteht aus einem viel zu komplexen System" hört man oft, wobei die Wörter wie System und Komplexität schon sehr Umgangssprachlich verwendet werden. Betrachten wir aber die Bedeutungen genauer, werden wir am Ende des Kapitels sehen, warum man mit Hilfe der Systemtechnik und den Nachfolgewissenschaften wie Regelungstechnik und Chaosforschung, diese Computerdinger präziser Beschreiben kann und auch deren Wirkungsweise besser verstehen kann.
Definition: Ein System ist eine Ganzheit aus
Definition: Die Komplexität eines Systems ist abhängig von
Beispiel:

Die Systemtechnik bietet eine "ganzheitlich-systematische
Vorgehensmethodik zum Lösen neuartiger, komplexer
Probleme".3)
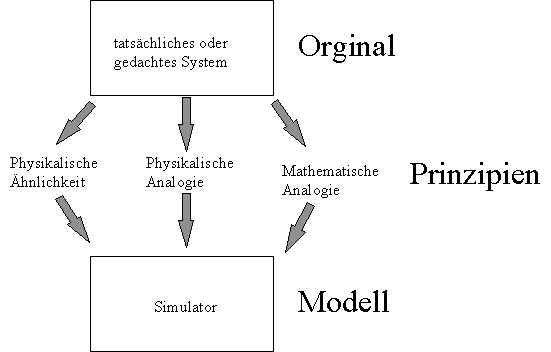
Um also obiges Beispiel besser betrachten zu können,
abstrahieren wir es aus der Realität und stellen es als Modell
dar. Das Modell ist dann die Abbildung eines realen Objektes
unter einem bestimmten Aspekt.
Beispiel: Betrachten wir bei obigen Billardkugel den Aspekt
der Lage der Billardkugel, so läßt sich ein mathematisches
Modell daraus bilden, welches dargestellt werden kann als
abstrakte graphische Darstellung:

Wie läßt sich nun solch ein Problem mathematisch darstellen?
Das Beispiel der Kugeln zeigt schon, daß für dieses, relativ
simpel anmutende System ein enormer Rechenaufwand betrieben
werden muß. Um es überhaupt als mathematisches Problem greifen
zu können, müssen wir auch viele Eingangsgrößen und
Komponenten des Systems vernachlässigen (Erwärmung der Kugeln,
Luftdruck...), die in die Berechnungen mit eingehen müßten.
Die gesamten Theorien der Physik sind ausschließlich Nährungen.
Kein mathematisches Modell kann ein universal gültiges Bild der
Realität (realen Welt) liefern. Außerdem funktioniert jede nur
innerhalb eines durch bestimmte Bedingungen definierten Bereichs,
außerhalb dessen die mathematischen Modelle unbrauchbar sind.
Dies ist für die Computer in doppelter Hinsicht kritisch, da
diese Modellbildung gleich zweifach angewendet wird. Einmal, wie
beschrieben, können die heutigen Computer nur als Systeme
betrachtet werden, die durch Kombination von Systemen mit
bekannten Ein- und Ausgangsgrößen zusammengesetzt werden.
Zum Anderen benutzen wir heutzutage Computersysteme
um die Realität zu simulieren, also
wiederum ein "vereinfachtes" Abbild der Wirklichkeit
schaffen um uns das Leben mit der "Wirklichkeit" durch
den Computer vereinfachen zu lassen.
Definition: Simulation:
Beispiele: Computerspiele, Flugsimulatoren, CAD, E-Sim, ...
Die Modellbildung ähnelt einem Kochrezept der Wirklichkeit. man versucht alle wichtigen Parameter eines Problems zu berücksichtigen (man nehme...) dann überprüfen die Computersysteme mit ihren Programmen, was passiert, wenn sich die Welt wie gewöhnlich verhält (gut umrühren und bei 350° backen). Die offensichtlich kritischen Punkte sind:
Das Modell oder die Simulation ist unter der Voraussetzung
hilfreich, daß die oben genannten Punkte mit Intelligenz,
Sachverstand und Logik durchdacht wurden. Trotzdem bleibt das Ganze
nur eine Vereinfachung der Realität. Das muß auch so sein:
Würde die Landkarte alle Details des dargestellten Gebietes
enthalten, wäre sie so groß wie das Gebiet selbst und aus
diesem Grund nutzlos. Die Aufgabe eines Modells besteht darin,
eine unendlich detaillierte Welt auf einige wichtige Details zu
reduzieren.
Die Experten, die das Modell oder die Simulation erstellen,
benutzen auch Vereinfachungen, deren Existenz erst zu Tage tritt,
wenn in einem eigentlich wichtigen Faktor vereinfacht wurde. Wird
dies offensichtlich, müssen die Ergebnisse der Simulation in
Frage gestellt werden. Dem Benutzer bleibt dann nichts anderes
übrig, als die berechneten Ergebnisse zu vergessen und sich
vollständig auf seinen menschlichen Verstand zu verlassen.
Der Wetterbericht ist ein Beispiel für die Datenmodellierung am
Computer. Die Tatsache, daß er häufig falsch ist, deutet darauf
hin, daß hier zu stark vereinfachte Modelle zugrunde gelegt
werden. Die Atmosphäre ist eine komplexe Ansammlung
verschiedener Phänomene, die wir noch (?) nicht verstehen.
Trotzdem ist der Wetterbericht ein im Grundsatz nützliches
System. Er enthält bereits selbst einen Hinweis auf seine
Zuverlässigkeit. "Diese Nacht liegt die
Regenwahrscheinlichkeit bei 50%". Ist der Wetterbericht
richtig entsteht ein trügerisches Zeichen von Sicherheit. Ist er
falsch stellt sich einem die Frage, was man schon dagegen
unternehmen könne. Wahrscheinlich wäre man zu Hause geblieben.
Die National Oceanic and Atmospheric Administration4)
betreut ein ganzes Netz von Wetterbojen entlang der US-Küste.
Dies Wetterbojen dienen als Datengrundlage für die Erstellung
der Sturmwarnungen. Die NOAA unterließ die Reparatur einer
einzelnen Boje. Aufgrund der fehlenden Daten konnte der National
Weather Service einen Sturm nicht vorhersagen. Drei Hummerfänger
fuhren aufs Meer hinaus und kamen nie zurück. Ihre Familien
zogen vor Gericht und erhielten 1985 ein Schmerzensgeld von 1,25
Mio. Dollar.
Wenn man die theoretischen Betrachtungen aus Kapitel 2.2.1
liest könnte man auf die Idee kommen, daß Krisen in
(Computersystemen) nur deshalb entstehen, weil man bei der
Erstellung der Modelle nachlässig war. Obwohl dies sicher auch
oftmals der Fall ist, so verhalten sich doch Systeme an sich
nicht immer vorhersagbar.
In der Systemtechnik benutzt man zu dieser Beschreibung Begriffe
wie "lineare Abhängigkeiten",
Nicht-Linearität".... welche in diesem Kapitel an
Beispielen erklärt werden sollen. (aus 5)):
Uhren zeigen für gewöhnlich die Zeit an. Aber nicht alle Uhren
machen dies mit der gleichen Genauigkeit.
Denken wir uns zunächst eine ideale Uhr, die die Zeit mit
hundertprozentiger Zuverlässigkeit anzeigt. Zunächst muß sie
gestellt werden. Wir rufen die Zeitansage an. Sie sagt uns die
Zeit bis auf die Sekunde:"Es ist drei Uhr, sechsundzwanzig
Minuten und dreißig Sekunden." Die Anfangsbedingung,
die wir auf unserer Uhr eintragen müssen, lautet: "Es ist
drei Uhr, sechsundzwanzig Minuten und dreißig Sekunden,
plus/minus eine Sekunde."
Bei einer hundertprozentig zuverlässigen Uhr ändert sich an
dieser Ungenauigkeit nichts. Vierundzwanzig Stunden später zeigt
sie die Zeit mit gleicher Genauigkeit an (plus/minus eine
Sekunde). Nach zwei, drei oder vier Tagen wird es noch genauso
sein.
In der realen Welt wird keine Uhr die Zeit mit solcher
Zuverlässigkeit anzeigen. In der Gebrauchsanweisung gibt der
Hersteller die Ganggenauigkeit seines Produktes an. Betrachten
wir den Fall einer zweiten Uhr, deren Ungenauigkeit eine Sekunde
pro Tag beträgt. Am Ende des ersten Tages werden wir die Zeit
bis auf zwei Sekunden genau kennen. Eine dieser Sekunden stammt
aus der Anfangsbedingung, die andere aus dem
Zuverlässigkeitsspielraum.
Die Unsicherheit der Uhrzeit wächst linear
mit der Zeit. Linear bedeutet hier nichts anderes, als daß sie
sich verdoppelt, wenn der betrachtete Zeitraum zweimal so groß
wird. Nach zwei, drei, vier Tagen wird die Ungenauigkeit
plus/minus drei, vier oder fünf Sekunden betragen.
Was nun die dritte Uhr betrifft, so gehen wir davon aus, daß die
Ungenauigkeit nicht, wie bei der zweiten, konstant bleibt (eine
Sek./Tag), sondern sich mit jedem Tag verdoppelt. Nach dem ersten
Tag eine Sekunde, nach dem zweiten zwei Sekunden usw.. Es liegt
also nichtlineares Wachstum vor. Wie
lange würde es nun dauern, bis die Ungenauigkeit zwölf Stunden
beträgt? Weniger als sechzehn Tage. Sechzehn Tage nachdem unsere
Uhr gestellt wurde, zeigt sie die Zeit mit einer Abweichung von
zwölf Stunden an. Sie ist völlig unbrauchbar.
Wie hängen nun diese Begriffe zusammen? Dies kann man wieder an
konkreten Beispielen zeigen. Die von einem Heizkörper
abgestrahlte Wärmemenge (Ursache) erzeugt eine bestimmte
Temperaturerhöhung (Wirkung). Wenn ich unter bestimmten
Bedingungen die Temperatur verdopple, verdopple ich auch die
Temperatur (in absoluten Gradeinheiten). Die Temperatur hängt
hier linear von der abgestrahlten
Wärmemenge ab.
Die Beschreibung gilt nicht für einen Waldbrand. Die durch die
Streichholzflamme bewirkte geringe Temperaturerhöhung genügt,
um einige dürre Äste zu entflammen. Dieser Brand setzt noch
mehr Wärme frei, erhöht die Temperatur weiter, usw.. Die
Intensität der Wirkung wirkt hier auf die Intensität der
Ursache zurück. Man bezeichnet das als Rückkopplungsschleife:
Die Ursache erzeugt die Wirkung, die Wirkung modifiziert die
Ursache, die wiederum die Wirkung modifiziert. Bei einem
Waldbrand hängt die Temperatur nichtlinear
von der vom Streichholz freigesetzten Wärme ab.
Der Vorhersagehorizont der
Temperaturentwicklung ist sehr kurz. Ein Waldbrand hat ein kaum
vorherzusagendes Verhalten.
Kommen wir nochmals auf das Beispiel der Wettervorhersage zurück. Wenn man das Beispiel in Kapitel 2.2.1 ansieht, könnte man zu dem Schluß kommen, man bräuchte nur stärkere Computer, um die Qualität der Wettervorhersage zu erhöhen. Das hat man lange geglaubt (siehe Laplace 6)).Doch dabei hat man übersehen das Gleichungen wie die der Aerodynamik extrem empfindlich für Anfangsbedingungen sind. Wenn wir also das Wetter berechnen wollen, das wir in einem Jahr haben werden, müssen wir zunächst alles einspeisen, was wir über den Zustand der Atmosphäre zum gegenwärtigen Zeitpunkt wissen: die Verteilung der Temperaturen, der Wolken, der Winde usw. Das Programm wird gestartet und errechnet: Schönes Wetter. Jedoch ist kurz nachdem wir das Programm gestartet haben, irgendwo auf der Welt ein Schmetterling aufgeflattert.. Man muß nun das Programm nochmals starten und diese neue Anfangsbedingung mit aufnehmen. Die Berechnungen nehmen einen völlig anderen Verlauf: Es regnet!
Als die Computersysteme noch einen so geringen
Kompexitätsgrad hatten, daß man mit Bestimmtheit von
deterministischen Systemen ausgehen konnte, mußte man den
Nachteil in Kauf nehmen, Computer nur in einem sehr begrenzten,
unnatürlichen Umfeld laufen zu lassen. Aber durch die
Möglichkeiten, natürliche Gegebenheiten zu simulieren und sich
gleichzeitig dem "nichtdeterministischen Benutzer"
anzupassen, muß in Kauf genommen werden, daß sich
Computersysteme auch nichtdeterministisch verhalten, auch wenn
eigentlich eine rein deterministische Handlungsweise gewünscht
wird.
Der Reiz des Computers wird jedoch bestimmt durch die Krisen die
dadurch hervorgerufen werden, wenn sich ein System nicht so
verhält, wie man eigentlich vorhersagen möchte. Wir betrachten
ein solches nichtdeterministisches Verhalten als natürlich und
kommen so in Versuchung, dem Computer ein Wesen zu geben (Mein
Computer liebt mich nicht mehr!).
Das Ergebnis einer Zusammenarbeit mit dem Computer wird also
bestimmt durch die Interaktion des unvorhersehbaren Menschen mit
der teilweise nicht vorhersehbaren Aktion der Computersystems.
Das sich hieraus ein Sozialverhalten zwischen Mensch und Maschine
entwickeln kann wird in den nächsten Kapiteln dargestellt.
© Matthias Marzinko 1997