



Next: Forschungsfeld,Nichtlineare Dymamik``
Up: No Title
Previous: Meinungen zu den
- Attraktor
-
Die Menge der Punkte im Zustandsraum, die nach unendlich langer Zeit
noch von Trajektorien erreicht werden, nennt man Attraktor des Systems.
- Bifurkation
-
Eine Bifurkation ist das plötzliche Auftreten einer qualitativ
anderen Dynamik bei langsamer Veränderung eines Kontrollparameters.
- Chaosforschung
-
Die Chaosforschung beschäftigt sich mit nichtlinearen Modellen und
mit Systemen, für die gezeigt werden kann, daß für diese lineare Modelle
unzureichend sind, mit der Ermittlung von Modellen für diese Systeme.
Zusätzlich werden allgemeine Prinzipien nichtlinearer Dynamik und
Kriterien für sinnvolle Fragestellungen an komplexe Systeme gesucht.
- Dendrit
-
Dendriten sind baumartig verzweigte Gebilde.
- Deterministisches Chaos
-
D.C. ist das scheinbar regellose dynamische Verhalten von Systemen.
Obwohl die zeitliche Entwicklung des Systems durch feste Regeln
determiniert ist, sind mittel- bzw. langfristige Vorhersagen des
Verhaltens aufgrund
der sensitiven Abhängigkeit von Anfangsbedingungen nicht möglich.
- Differentialgleichung
-
Eine gewöhnliche Differentialgleichung
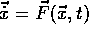 ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
- diskretes Modell
-
Bei diskreten Modellen werden statt kontinuierlichen Variablen für
Zeit, Raum und/oder die Zustandsgrößen diskrete Variablen verwendet.
Diskrete Modelle für nichtlineare Dynamik sind z.B. stroboskopische
Abbildungen
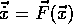 , diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
, diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
- dissipatives System
- System mit Reibung oder Dämpfung. Diese
Systeme haben (mindestens) einen Attraktor. Gibt es genau einen Attraktor,
dann spielt die Anfangsbedingung für das globale Verhalten der Dynamik der
Systems keine Rolle.
- Fixpunkt
-
Punkt im Zustandsraum, der nicht verlassen wird, wenn er einmal exakt
erreicht wurde. Bei stabilen Fixpunkten nähern sich die Trajektorien
immer weiter an den Fixpunkt an. Das Kriterium für Fixpunkte bei
Differentialgleichungen (
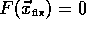 ) ist
) ist
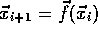 ,
bei Abbildungen (
,
bei Abbildungen (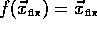 ) gilt:
) gilt:

- Interdisziplinäre Chaosforschung
-
Die betrachteten Systeme stammen aus allen Gebieten der Wissenschaft und des
täglichen Lebens, für die quantitative Modelle für deren Dynamik sinnvoll
erscheinen. Die Bewertung von mathematischen Methoden und Begriffen
geschieht in enger Zusammenarbeit mit den Anwendungsdisziplinen.
- Nichtlinearität
-
Ggs. zu Linearität. Lineare Systeme verhalten sich qualitativ gleich,
wenn die Zustandsvariablen um einen beliebigen konstanten Faktor
vergrößert oder verkleinert werden. Lineare Systeme haben keine
charakteristische Größe für die Zustandsvariablen.
- NP-hartes Problem
-
NP-harte Probleme liegen vor, wenn man beweisen kann, daß die
Zahl der benötigten Rechenoperationen für eine algorithmische Lösung
bei einem beliebig herausgegriffenen Beispielproblem stärker
als durch eine Polynom-Funktion beschreibbar mit der Komplexität
der Problemstellung (=Zahl der Unbekannten, Dimensionen, etc.) anwächst.
- Rauschen
-
Sammelbegriff für alle nicht näher auflösbaren und daher nur statistisch
zu beschreibenden dynamischen Vorgänge.
Es gibt Meßrauschen (statistische Meßfehler),
Systemrauschen (nicht betrachtete Freiheitsgrade) und externes Rauschen
(z.B. Straßenbahn). In welchen Fällen nicht dominante Freiheitsgrade
als Systemrauschen und wann als Zustandsvariablen behandelt werden
sollen ist ein typisches Problem der Chaosforschung.
- Resonanzspektroskopie
-
Bei der R. wird ein System hintereinander mit verschiedenen Signalen angeregt,
wobei sich die Signale durch einen Parameter unterscheiden. Tritt bei einem
Parameterwert ein außerordentlich hoher Response auf, ist dieser Wert
charakteristisch für die Eigendynamik des Systems.
- Trajektorie
-
(=Bahnkurven.) Die Menge von Punkten im Zustandsraum, die nacheinander von der
Dynamik des Systems erreicht werden.
- zellulärer Automat
-
Ein zellulärer Automat ist ein Kristall aus Zellen, deren diskrete Zustände
sich zeitlich verändern. Der Zustand im nächsten Zeitschritt ergibt
sich durch eine deterministische Regel aus dem alten Zustand und dem
Zustand der nächsten (evtl. auch übernächsten) Nachbarzellen.
- Zustandsraum
-
Raum, der von den Zustandsvariablen des Systems aufgespannt wird.
Die Zustandsvariablen sind ein Satz von Zahlen, durch den der
Zustand des Systems eindeutig beschrieben wird. Kann man nicht
alle realen Zustandsvariablen messen, verwendet man als
Ersatzvariablen Zeitableitungen oder zeitverzögerte Zustandsvariablen.




Next: Forschungsfeld,Nichtlineare Dymamik``
Up: No Title
Previous: Meinungen zu den
Werner Eberl
Sat Apr 15 13:17:50 MET DST 1995
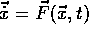 ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
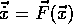 , diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
, diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
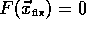 ) ist
) ist
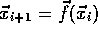 ,
bei Abbildungen (
,
bei Abbildungen (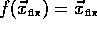 ) gilt:
) gilt:





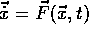 ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
ist eine Vorschrift, die angibt, in welche Richtung sich ein Zustand im
infinitesimal nächsten Zeitschritt entwickelt
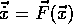 , diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
, diskrete Modelle für
Dynamik in Raum und Zeit sind z.B. zelluläre Automaten.
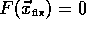 ) ist
) ist
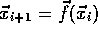 ,
bei Abbildungen (
,
bei Abbildungen (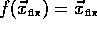 ) gilt:
) gilt:




