
In dieser Arbeit:
1. Erstellung von Fraktalen mit IFS
1.2. Iterierte Funktionensysteme als einfache Abbildungsmaschine
1.3. Kompression und "unendlicher" Zeitaufwand - das Problem des Codierens
2. Kompression von digitalisierten Bildern
2.1. Eine Abbildungsmaschine für beliebige Bilder
2.2. Bildcodierung - Auffinden des Codes mit einem Algorithmus
3. Literaturverzeichnis und Abbildungsverzeichnis
Multimedia, digitale Kommunikation, World Wide Web - Schlagworte, die heute und in Zukunft nicht mehr wegzudenken sind. Besonders das Internet zieht viele vor allem junge "user" an, die sich mit seiner Hilfe mit Informationen eindecken. An allen Universitäten und Hochschulen sieht man viele begeisterte Studenten an den Terminals sitzen und im Web "surfen". Eine große Anzahl neuer Texte und das Wichtigste: vor allem Bilder eröffnen sich dem Betrachter. Wer will sich denn heute schon mit einer Textseite ohne bunte Bilder zufriedengeben? Ja, einige schon. Viele Benutzer wollen sogar beim Anwählen einer neuen Seite verhindern, daß ihre Bilder aufgebaut werden. Warum dieses seltsame Verhalten? Weil es nach Ansicht vieler Internetbenutzer "ewig" dauert, bis die Bilder und damit die Seite komplett ist. Das Problem liegt in der Datenmenge, die übertragen werden muß und in der limitierten Leistungsfähigkeit der Übertragungsnetze. Trotz kleinerer Bildformate und Komprimierungsmechanismen lassen sich noch nicht genügend Informationen in genügend kurzer Zeit übertragen. Also versucht man, die Datenmengen mit geeigneten Mitteln noch weiter zu reduzieren.
In dieser Arbeit soll eine Komprimierungsmethode
für Bilder vorgestellt werden, mit der es möglich ist,
die Bilder auf dem Bildschirm "berechnen" zu lassen.
Anstatt ein digital gespeichertes Bild Pixel für Pixel mit
seinen Grauwerten abzuspeichern, werden diese Werte aus den Parametern
einer Funktion errechnet. Diese Methode nennt sich IFS: Iterierende
Funktionensysteme.
1. Erstellung von Fraktalen mit IFS
Klassische Fraktale eignen sich besonders gut für die Codierung mittels Systemen von Funktionen, denn sie lassen sich meist durch eine einfache Abbildungsvorschrift erstellen. Eine Abbildungsvorschrift für die Koch-Kurve zum Beispiel lautet:
Man nehme eine Strecke, teile sie in 3 Strecken der Länge l und nehme die Mittlere heraus. Danach setze man auf das fehlende Stück in Form eines Daches 2 Strecken mit ebenfalls der Länge l . Auf die entstandenen 4 Strecken wende man wiederum die Vorschrift an, usw. (siehe Abb. 1 ).
Diese Vorschrift läßt sich auch als ein System mathematischer Funktionen ausdrücken, wobei diese Vorschrift ständig wiederholt wird. Die Ausgangsgrößen sind jeweils Eingangsgrößen für die nächste Iteration, wobei diese Ein- und Ausgangsgrößen Bilder darstellen, das heißt, zweidimensionale Strukturen. Das Ergebnis dieses Beispiels wird die Koch-Kurve sein.
Was ist das Besondere an diesen klassischen Fraktalen?
Es ist ihre Selbstähnlichkeit, d. h. ein kleiner Teil dieser
Kurve sieht vergrößert genauso aus wie das Gesamtbild.
Diese Eigenschaft entsteht zwangsläufig durch die wiederholte
Anwendung der Abbildungsvorschrift. Das Urbild wird bei einer
Transformation jeweils 4-mal abgebildet, d.h., jedes Ausgangsbild
besteht aus 4 Eingangsbildern und auch diese bestehen aus 4 Eingangsbildern
der vorherigen Iteration. Und genau deshalb - nämlich weil
die Koch-Kurve ein selbstähnliches Fraktal ist - läßt
sie sich durch die Parameter einer einzigen Abbildungsvorschrift
darstellen.

Abb.1 : Die Koch-Kurve
1.2 Iterierte Funktionensysteme als einfache
Abbildungsmaschine
Der Aufbau eines Bildes aus einem System von Funktionen soll hier nun etwas genauer beleuchtet werden. Was sind Funktionensysteme, und wie kann man daraus - zunächst nur einfache - Bilder gewinnen und wie sehen diese Funktionensysteme aus? Diese Fragen sollen nun geklärt werden.
Nehmen wir an, die Abbildungsvorschrift sei bereits bekannt, wie es bei den bekannten Fraktalen der Fall ist. Wie läßt sich daraus ein Bild erzeugen? Eine Abbildungsvorschrift wie oben beschrieben : "...Strecke teilen..." läßt sich wie bereits erwähnt auch in mathematischer Form als eine Funktion w darstellen:
wobei x die Punkte der Strecke sind.
Das Bild der Strecke , der Graph der Funktion w(x), wird nun viermal an bestimmten Orten abgebildet, dabei wird es auch gedreht. Auch dafür gibt es eine mathematische Schreibweise, sie ist nur etwas komplizierter. Um die räumliche Lage der Strecke und ihrer Bilder w(x) darzustellen, benötigt man zwei Dimensionen. Man muß die Vorschrift w also auf zwei Koordinaten anwenden, um die Strecke zu drehen und sie viermal an ihren Bestimmungsorten abzubilden.
Mathematisch geschieht das durch Aufteilen der Abbildungsvorschrift
in zwei Vorschriften, die jeweils verschieden auf die Koordinaten
wirken, und ein zweidimensionales Bild erzeugen.
Dies ist eine Funktion von zwei Variablen.
Die Abbildungsvorschrift w
hat dann die Form
wobei x und y die Koordinaten der Bildpunkte des
Eingangsbildes P, und u und v die der Ausgangsbilder w(P) sind.
In dieser Schreibweise lassen sich alle sogenannten affinen Transformationen
darstellen. Affine Transformationen sind folgende Abbildungen:
Skalierung (d.h. schrumpfen oder strecken) , Scherung, Drehung,
Spiegelung und Verschiebung. Die Parameter dieser Transformationen
werden in Matrizen sehr kompakt zusammengefaßt. Auch lassen
sich in einer Matrix mehrere Transformationen zusammenfassen,
indem man die Matrizen einfach Multipliziert.
Die Teilung, Drehung und Plazierung einer Strecke kann somit in
einem Zug, also mit nur 6 Parametern a,b,c,d,e und f vorgenommen
werden.
Damit ist die Abbildungsvorschrift mit 6 Parametern mathematisch
codiert.
In dem Beispiel der Koch- Kurve soll nun die Strecke viermal an
verschiedenen Plätzen in unterschiedlicher Weise gedreht
dargestellt werden. Dies erreicht man, indem man 4 verschiedene
Abbildungsvorschriften nacheinander auf das Anfangsbild, eine
Strecke, anwendet. Peitgen, Jürgens und Saupe verwenden
hier die Metapher einer Mehrfach-Verkleinerungs-Kopier-Maschine,
eine einfache Abbildungsmaschine, die mit einer Anzahl von n Linsen
n verkleinerte und transformierte Abbildungen des Originals auf
eine Kopie druckt. Danach wird die Kopie mit den n Abbildungen
wiederum als Anfangsbild benutzt. Dies ist eine schöne anschauliche
Beschreibung des IFS. Im Beispiel der Koch- Kurve bestündedie Maschine aus 4 Linsen, die die Anfangsstrecke unterschiedlich
drehen ind plazieren. Eine mathematische Darstellung der 4
Transformationen,
die hintereinandergeschaltet werden, hat folgende Form:
W wird der Hutchinsonoperator genannt. Die wi stellen die verschiedenen Transformationen der Ausgangsstrecke dar. Der Hutchinsonoperator setzt sich also aus mehreren Funktionen wi zusammen, stellt also ein Funktionensystem dar, das das Endprodukt eines Durchlaufs wieder als Eingangsprodukt einsetzt: Hier haben wir unser Iterierendes Funktionensystem.
Um das fertige Endbild zu erreichen, werden die Iterationen so lange fortgesetzt, bis kein Unterschied zwischen den Bildern aus zwei aufeinanderfolgenden Iterationen zu erkennen ist, das heißt, bis das Bild unter W invariant bleibt.
Doch wann kann man keinen Unterschied mehr zwischen zwei Iterationen feststellen?
D.h.wann ist der Unterschied zwischen zwei Bildern klein genug? Sicherlich
dann, wenn die Darstellung ihre Auflösungsgrenze erreicht
hat, d.h. wenn eine weitere Iteration keine neuen Details mehr
zeigen kann, denn diese liegen dann innerhalb der Pixelgröße.
Der Unterschied zweier Bilder läßt sich
auch mathematisch ausdrücken. Dazu wird der Hausdorff-Abstand
zweier Punktemengen definiert,worauf hier nicht weier eingegangen werden soll.
[ Peitgen,Fraktale..., S. 321]
Damit nach genügend vielen Iterationen der
Abbildung der Abstand zweier Bilder möglichst klein ist,
muß die Funktion eine grundlegende Bedingung erfüllen:
Sie muß die Ausgangsbilder verkleinernd auf die Kopie abbilden.
In mathematischer Ausdrucksweise heißt das: Die Abbildung
ist kontrahierend, also zusammenziehend.
Wenn das Bild schließlich invariant unter der Abbildung bleibt, so ist das Endbild, der sogenannte Attraktor, erreicht. Der Attraktor unserer Abbildung ist die Koch- Kurve.
Wie sieht nun konkret so ein IFS für ein klassisches Fraktal aus? Man findet die Parametera,b,c,d,e und f, d.h. den Code, für ein IFS, dann sehr einfach, wenn man die Abbildungsvorschrift des Fraktals kennt. Dies ist auch bei dem folgenden Beispiel, dem Farn von Abb. 2 der Fall. Barnsley codiert ihn durch nur vier Transformationen wi, indem er wiederumdie Selbsähnlichkeit des Farns ausnutzt. In der Tab.1 sind die Parameter a,b,c,d,e und f für das IFS des Barnsley-Farns zusammengestellt. Die Parameter a-d bedeuten hier die Stauchungen und Drehungen, Die Parameter e und f die Verschiebung des Bildes auf seinen neuen Platz.
Abb.2: Barnsleys Farn
| w | a | b | c | d | e | f |
| 1 | 0 | 0 | 0 | 0.16 | 0 | 0 |
| 2 | 0.85 | 0.04 | -0.04 | 0.85 | 0 | 1.6 |
| 3 | 02 | -0.26 | 0.23 | 0.22 | 0 | 1.6 |
| 4 | -0.15 | 0.28 | 0.26 | 0.24 | 0 | 0.44 |
Tab. 1: Die Parameter für das IFS des Barnsley-Farns
[Peitgen, Fraktale...S.306] Die Abbildungsmaschine von Peitgen, Jürgens und Saupe
würde auch hier mit nur 4 Linsen für die vier Transformatonen
wi arbeiten. Die Transformationen
1 und 2 sind jeweils nur eine Drehung mit Verkleinerung, Transformation
3 hat zusätzlich eine Spiegelung und die 4. Ist eine Stauchung
in nur eine Richtung , so daß als Stil des Farns nur ein
Strich übrigbleibt.
Um das Bild nun aufzubauen, braucht man die Abbildungsmaschine nur wiederholt mit einem beliebigen Anfangsbild laufen zu lassen. Als Anfangsbild soll hier ein Rechteck dienen.
Die erste Iteration sieht man auf der Abbildung Nr. 3. Hier ist das Grundgerüst zu sehen, an dem man erkennt, wie die Transformationen wirken. Diesen Bauplan kann man auch umgekehrt dazu nutzen, den Code für das Bild zu finden, bzw. zu errechnen. Dies geschieht, indem man zuerst dieses Grundgerüst aus dem Endbild von Hand zeichnet, aus dem sich dann die Transformationen ableiten lassen. Man findet dieses Grundgerüst, indem man selbstähnliche Strukturen sucht, wie die untersten Blätter und der Stil ( indirekt ist er auch selbstähnlich) und eine Karte aus diesen transformierten Abbildungen der gesamten Struktur zusammensetzt. der Code errechnet sich dann aus den Transformationen, die für diese Abbildungen nötig waren.
Die Abbildung Nr. 4 zeigt den Barnsley- Farn nach 5 bzw. nach
10 Iterationen. Man kann das Grundgerüst sehr gut erkennen,
und wie das Anfangsrechteck mit zunehmender Zahl der Iterationen
immer kleiner wird und mehr Details des Farns sichtbar werden.
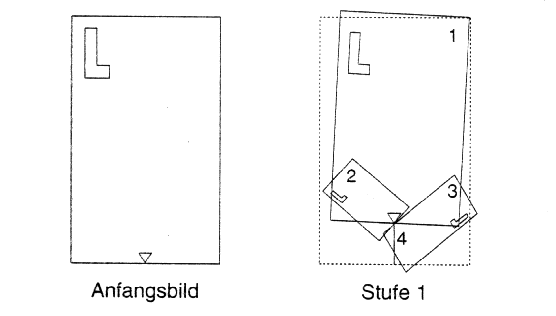
Abb. 3. Grundgerüst des Barnsley- Farns.

Abb. 4: Die 5. und 10. Iteration des IFS.
Im Folgenden seien noch einige weitere Beispiele für ein
IFS zusammen mit ihren Attraktoren (Das Endbild, das durch eine weitere Iteration
nicht mehr verändert wird)
gezeigt. Die Tabelle 2 gibt die zugehörigen Parameter für
die Transformationen der IFS an. Damit lassen sich die folgenden
Bilder erzeugen:

Abb. 5: Eine Schneeflocke, zusammengesetzt aus vier Abbildungen.

Abb. 6 : Ein Baum, bestehend aus fünf Transformationen.
Die dreieckige Schneeflocke ist aus 4 Transformationen zusammengesetzt, wobei drei davon nur eine Schrumpfung in beiden Richtungen um den Faktor 0.255 und eine Verschiebung enthalten. Die vierte Transformation besteht aus einer Drehung und einer Schrumpfung um den Faktor 0,37.
Das IFS des Baumes wiederum setzt sich aus 5 Transformationen zusammen, und sie entwerfen ein erstaunlich wirklichkeitsnahes Bild.
Die Geometrischen Figuren in Abb. 8 zeigen, daß nicht alle
Objekte durch ein IFS gut dargestellt werden können: Der
Kreis, wenn er mit IFS codiert wird, ist nicht exakt. Man kann
ihn mit dieser Methode nur annähern.

Abb. 7 : Fünf Ähnlichkeitstransformationen für eine fünfeckige
Schneeflocke

Abb. 8 : Die Darstellung geometrischer Figuren mit einem IFS. Der Kreis ist mit vier Transformationen nur mangelhaft darstellbar
| Abb | w | a | b | c | d | e | f |
| 5 | 1 | 0.255 | 0 | 0 | 0.255 | 0.3726 | 0.06714 |
| 2 | 0.255 | 0 | 0 | 0.255 | 0.1146 | 0.2232 | |
| 3 | 0.255 | 0 | 0 | 0.255 | 0.6306 | 0.2232 | |
| 4 | 0.370 | -0.642 | 0.642 | 0.370 | 0.6306 | -0.0061 | |
| 6 | 1 | 0.195 | -0.488 | 0.344 | 0.443 | 0.4431 | 0.2452 |
| 2 | 0.462 | 0.414 | -0.252 | 0.361 | 0.2511 | 0.5692 | |
| 3 | -0.058 | -0.070 | 0.453 | -0.111 | 0.5976 | 0.0969 | |
| 4 | -0.035 | 0.070 | -0.469 | -0.022 | 0.4884 | 0.5069 | |
| 5 | -0.637 | 0 | 0 | 0.501 | 0.8562 | 0.2513 | |
| 7 | 1 | 0.382 | 0 | 0 | 0.382 | 0.3072 | 0.6190 |
| 2 | 0.382 | 0 | 0 | 0.382 | 0.6033 | 0.4044 | |
| 3 | 0.382 | 0 | 0 | 0.382 | 0.0139 | 0.4044 | |
| 4 | 0.382 | 0 | 0 | 0.382 | 0.1253 | 0.0595 | |
| 5 | 0.382 | 0 | 0 | 0.382 | 0.4920 | 0.0595 |
Tab.2: Die Parameter des IFS für die obigen Abbildungen [Peitgen, Fraktale...S.350]
1.3. Kompression und "unendlicher"
Zeitaufwand -
das Problem des Codierens
Um wieviel läßt sich die Datenmenge komprimieren, wenn ein Bild - hier ein klassisches Fraktal - mit IFS codiert wird?
Am Beispiel des Baumes aus dem vorherigen Kapitel ( Abb.6) kann man die Kompression der Datenmenge,d.h. das Kompressionesverhältnis errechnen. Das Kompressionesverhältnis bedeutet das Verhältnis von gespeicherter Datenmenge ohne Codierung zu der Datenmenge mit codierung. Die Datenmenge eines Bildes ohne Codierung mit n x m Pixeln beträgt 8 x n x m bit, wenn für jedes Pixel ein gespeicherter Grauwert in einem 8-bit Wort (256 Graustufen) abgespeichert wird, bzw. nur nxm bit für ein Bild mit nur schwarzen und weißen Objekten. Das mit IFS codierte Bild dagegen benötigt nur die Datenmenge für die sx6 Parameter, die die s Transformationen w(P) mit ihren 6 Parametern festlegen. Bei dem Baum ist s = 5. Wenn man eine reelle Zahl mit einem 32- bit-Wort speichert, dann braucht man für das gesamte Bild 5x6x32 bit = 960 bit. Das Kompressionsverhältnis bei einem 1000x1000 Pixel großem Bild ist also von der Größenordnung 8x1000x1000 / 960 = 8300 oder für reine s-w-Bilder ca. 1000. Der Baum wird unter IFS also um das 1000-fache der ursprünglich zu übertragenden Datenmenge komprimiert.
Eine solch phantastische Kompression ist natürlich nur möglich, wenn eine einfache Abbildungsvorschrift mit möglichst wenigen Transformationen vorliegt. Komplexere Bilder können verständlicherweise nicht nur mit einigen wenigen Transformationen "errechnet" werden, sie sind ja nicht in allen ihren Teilen sich selbst ähnlich.
Mit diesen komprimierten Daten kann man nun mit einem Computer das codierte
Bild decodieren und sichtbar machen. Man muß dem Computer
nur ein beliebiges Anfangsbild und das IFS eingeben. Der Attraktor
ist dann unabhängig vom gewählten Anfangsbild, denn
bei jedem weiteren Durchgang der Abbildungsmaschine wird das Ausgangsbild
immer weiter verkleinert, bis es schließlich Pixelgröße
erreicht hat und nicht mehr zu erkennen sind. Das Endbild (der
Attraktor) bleibt also für ein IFS immer das gleiche.
Die nächste Frage ist: Wie oft muß die Maschine die Abbildungsvorschrift wiederholen, d.h. wie viele Iterationen sind notwendig, um das Bild gut genug darzustellen?
Nimmt man an, daß im Endbild kein Anfangsbild mehr zu erkennen sein soll, z.B. ein Rechteck (vgl. der Farn auf Abb.3), so müssen hier die Anfangsrechtecke die Größe eines Pixels erreichen. Peitgen, Jürgens und Saupe führen sehr schön vor, wie lange ein Computer rechnen muß, um das zu erreichen [ Peitgen, Fraktale....S. 311]: nämlich 10 hoch 10 Jahre!
Das Problem der Datenübertragung hat sich also zu einem Problem des Bildaufbaus im Computer verschoben.
Offenbar ist das IFS doch noch eine etwas unzureichende Methode der Bildcodierung. Um die Rechenzeit zu verkürzen, kann man entweder die Transformationen ändern (z.B. für jedes Pixel eine eigene Funktion). Damit ist aber nichts erreicht. Oder man versucht, von dem Anfangsrechteck abzugehen und das Anfangsbild dem Endbild anzunähern. Doch dann muß dieses Anfangsbild ebenfalls abgespeichert werden, was wiederum die Datenmenge erhöht. Dies sind beides nicht zufriedenstellende Methoden.
Diese Probleme des Bildaufbaus lassen sich aber dennoch durch
Umwandlung des Algorithmus' ( statt Rechtecke werden dann nur
Punkte gezeichnet) in den Griff bekommen. Doch diese Algorithmen
sollen hier nicht weiter besprochen werden.
Wie man ein Bild mit IFS speichern und mit Computerprogrammen decodieren kann, wurde bereits gezeigt. Doch wie findet man den richtigen Code d.h. die Parameter der Transformationen für ein erwünschtes Fraktal? Dies ist das Problem des Codierens.
Abb. 9 : Eine Ähnlichkeitstransformation eines Ahornblatts.
Bei etwas komplexeren Bildern, die aber immer noch einen gewissen Teil an Selbstähnlichkeit besitzen, kann man eine andere Methode anwenden, um den Code zu finden: Die Collage. Damit lassen sich auch nicht-fraktale Bilder erzeugen. M.F. Barnsley beschreibt diese Methode in seinem Buch [Barnsley,Fraktale,S.108ff].
Der Trick besteht darin, das Zielbild mit mehreren verkleinerten und verzerrten (sprich transformierten) Abbildungen seiner eigenen Kontur zu überdecken. Beim Farn würde also ein Mehreck, das den Farn umschließt, verkleinert, und dann mehrmals auf seinen eigenen Umriß abgebildet, solange, bis der Farn von seinen eigenen Verkleinerungen vollkommen überdeckt ist. (vgl.Abb. 10)

Diese Methode läuft nicht automatisch , der Computer braucht
noch einen Menschen, der den Umriß des eingescannten Bildes
festlegt, dann den Polygonzug mit der Maus oder der Tastatur transformiert
( mit Graphikprogrammen heute kein Problem) und an die richtige
Stelle postiert. Hat man schließlich das Bild vollständig
überdeckt, so liefert der Computer die Parameter der ausgeführten
Transformationen und der Code des IFS ist gefunden. Man kann dann
das Bild mit einem beliebigem Anfangbild wieder dekodieren. Auf
Abb.11 ist die Collage eines Blattes, die aus vier Transformationen
seines Umrisses besteht, zusehen. Der Attraktor ist ein Ahornblatt.
Abb. 11 : Collage eines Blattes: der Umriß des Blattes
wird mehrmals transformiert und auf seinen eigenen Umriß
abgebildet, bis das Blatt vollständig überdeckt ist.
Abschließend zum ersten Kapitel sei noch bemerkt, daß sich viele weitere, nicht unbedingt fraktale Objekte durch einen umgeänderten Algorithmus darstellen lassen.Man kann das IFS etwa auch auf 3 Dimensionen erweitern und erhält damit plastische Objekte. Auch kann man einen Algorithmus entwerfen, der unterschiedliche Transormationen anwendet: beim 1. Durchlauf ein erster Satz von Transformationen w , beim 2. dann einen anderen w , danach folgt wieder der erste usw. Das Ergebnis ist auch ein Fraktal, doch es ist sich nicht in allen seinenTeilstücken komplett ähnlich, sondern es decken sich nur bestimmte Vergößerungen mit dem gesamten Bild.
So erhält man ein großes Spektrum von Fraktalen, die sich mit IFS darstellen lassen. Doch wie bereits das Beispiel des Kreises (siehe Abb. 8) gezeigt hat, ist diese Methode nicht immer optimal für die Speicherung sämtlicher Objekte.
Was sich Y. Fisher (Yuval Fisher's
Fractal Image Encoding Page) hat einfallen lassen, um ganz gewöhnliche
Photos oder Bilder zu codieren, und damit zu komprimieren, wird
das Thema des 2. Kapitels sein. [Peitgen, Fraktale...S.473ff]
2. Kompression von digitalisierten Bildern
2.1. Eine Abbildungsmaschine für beliebige
Bilder
Im ersten Kapitel wurde gezeigt, wie man zunächst klassische Fraktale und später auch fraktal-ähnliche Bilder mit der Collagemethode mittels IFS codieren kann. Alle Bilder waren in gewisser Weise selbstähnlich. Doch was, wenn man ganz ordinäre Bilder codieren will?
Viele natürliche Objekte wie Berge, Seen, Pflanzen enthalten Teile, die selbstähnlich sind, z.B. die Wellen der Seeoberfläche oder die Äste und Zweige eines Baumes, und diese Ähnlichkeiten werden zur Komprimierung auch ausgenutzt. Doch eine Katze, Maus oder ein Portrait haben wenig mit den bisher verwendeten und codierten Bildern gemeinsam. Hier behilft man sich - das ist das Kernstück der Codierung - mit der Suche nach selbstähnlichen Teilen der Figur. Anstatt Abbildungen des Ganzen auf eine Kopie zu plazieren, wird hier ein Bild aus Teilen des Ganzen aufgebaut. Diese Methode ist komplizierter und soll daher nur prinzipiell erklärt werden.
Fast in jedem Objekt findet man Stellen, die sich ähneln, wie gerade und gebogene schwarz-weiß-Kontraste, dünne dunkle Linien vor hellem Hintergrund, oder einfach graue Bereiche. In Abb. 12 , "Lenna " , sind einige solcher selbstähnlicher Bereiche gezeigt.
Abb. 12 : Sich ähnelnde Bereiche in "Lenna"
Wie baut sich nun ein Bild auf, wenn der Code bereits bekannt ist? Wie sieht der Mechanismus beim Decodieren aus?
Dazu wird eines dieser ähnlichen Stücke herausgegriffen (bisher wurde das ganze Bild herausgegriffen), transformiert, und an einer bestimmten Stelle der Kopie wieder abgebildet, die der ersten eben nun mal ähnlich sieht. Und nicht jedes einzelne Teilstück des Endbildes muß auch ein Anfangsbild einer Transformation sein. Man legt also eine Art Maske an, die die Abbildungsvorschrift wi auf einen gewissen Teil Di des Gesamtbildes einschränkt. Nur dieser Teil des Bildes wird unter wi transformiert und auf der Kopie als Ri abgebildet.
Auch diese Maschine arbeitet in einer Rückkopplungsschleife,
d.h. dieser Vorgang wiederholt sich.
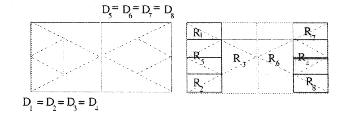
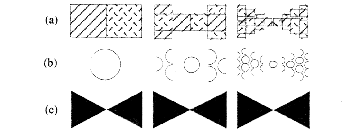
Abb. 13: Die "Fliege"
Ebenso kann auf den Bereich, der als Urbild Di diente, ein anderes transformiertes Bild Rj abgebildet werden . In der nächsten Iteration ist dann eben diese Abbildung Rj das neue Urbild Di, das mit wi wieder transformiert wird. Auf den Platz von Di tritt wiederum das Bild der Abbildung Rj. Auf diese Art wird auf mehrere Teilstücke Einfluß genommen.
Des weiteren muß natürlich jedes Stück aus dem gesamten Bild ein Endbild Ri sein, so daß sie ein komplettes Endbild ohne Lücken ergeben. Ein einfaches Beipiel für diese Methode zeigt Fisher in Abb.13.
Hier liegen 8 Transformationen vor w1 ....w8 , die jeweils die eine oder andere Hälfte des Bildes als Urbild Di haben. Aber ihre Abbildungsbereiche liegen verstreut in den Teilbereichen R1...R8. Man erkennt, daß auch die Urbildbereiche D1=2=3=4 und D5=6=7=8 mehrfach verwendet werden können. Auch wird jeder Urbildbereich bei jeder Iteration aufs Neue verändert. Der Attraktor ist hier stets eine Fliege. Man sieht an diesem Beispiel, wie sich mit jeder weiteren Iteration immer mehr Details bilden. Da die Bildbereiche Ri kleiner gewählt sind als die Urbildbereiche, werden die Strukturen immer kleiner und daher das Bild detaillierter.
Nun bestehen aber reale Bilder nicht nur aus Schwarz-weiß-Details, sie enthalten ebenso graue Flächen oder Verläufe ( der Einfacheit halber beschränkt man sich hier auf s-w-Bilder. Farbige Objekte lassen sich mit Erweiterungen des Algrithmus' auch herstellen. Dies soll aber hier nicht gezeigt werden.).
Das Bild wird deshalb als Graph einer Funktion von Grauwerten beschrieben. Man kann sich diese Funktion f(x,y)=z (=Grauwert) als ein Gebirge vorstellen, das sich über den Bildkoordinaten (x,y) aufbaut. Je höher das Gebirge, desto heller der Pixel an dieser Stelle. (S. Abb. 14).
Abb. 14 : Ein Bild als Graustufenfunktion
Um die Graustufen in der Abbildungsvorschrift des Funktionensystems
ebenfalls abspeichern zu können, und auch die Grauwerte eines
Bildbereichs mit der Transformation verändern zu können,
werden im Funktionensystem neue Parameter eingeführt: s und
o für Kontrast und Helligkeit. Die Transformation wi wird
also um eine Dimension erweitert und sieht dann so aus:
Das gesamte IFS hat dann die folgende Form:
P ist in diesem Falle das gesamte Anfangsbild, das dieselbe Größe wie das gesamte Endbild hat. Die Transformationen wi wirken auf verschiedene Teile Di des Anfangsbildes, die sich auch überlappen können und größer oder gleich dem Abbildungsbereich Ri sein können. Die gesamte Abbildungsvorschrift W wird nun wiederholt angewendet, bis das Endbild erreicht ist. Dieses wird dann der Attraktor des IFS, oder auch Fixpunkt genannt, da es unter der Abbildung W unverändert, also fix bleibt.
Wie oft muß nun die Abbildung W wiederholt werden, d.h. wie viele Iterationen sind notwendig für ein gutes Bild?
Dafür muß solange solange iteriert werden,
bis sich die entstehenden Bilder
W(P) nicht mehr unterscheiden.
Um den Unterschied zweier Bilder zu messen, wird auch hierfür
mathematisch der "Abstand
" zwischen zwei Bildern bestimmt. Das ist dann der Unterschied
zwischen den Werten der Graustufenfunktion f(x,y). (Tatsächlich
berechnet man nicht die Differenz der Werte f(x,y) nach n Schritten
und f(x,y) nach n+1 Schritten, sondern wendet die Methode der
kleinsten Quadrate an).
Bei jedem Durchlauf der Abbildungsmaschine (bei jeder weiteren Anwendung der Abbildungsvorschrift) nähert sich das Bild seinem Attraktor an. Dieser Attraktor wird zwar nicht genau das Originalbild darstellen, doch es wird eine gute Näherung sein. So hat der Attraktor beispielsweise nicht die gewohnte Pixelstruktur mit einem gleichen Grauwert über den gesamten Pixel. Vielmehr ist ja ein Bildbereich Ri aus transformierten Urbildbereichen entstanden, so daß hier auf der Größe eines Pixels auch verschiedene Grauwerte zu finden sind, wenn man beide Bilder vergrößert.
Hier zeigt sich eine erstaunliche Eigenschaft der mit IFS decodierten Bilder:
Sie sind unabhängig von der Auflösung. Bei jeder Vergrößerung wird das decodierte Bild Details zeigen, die von den Transformationen erzeugt worden sind. Die erzeugten Details sind natürlich nicht immer identisch mit den tatsächlichen Details; man wird z.B. keine Hautporen oder gar Zellen erkennen können. Doch bis zu einem gewissen Grad der Vergrößerung (der nicht sehr groß ist), sind die erzeugten Details sehr wirklichkeitsnah. In Abb.15 ist bei 4-facher Vergrößerung im nicht codiertem Bild noch Pixelstruktur zu erkennen, im codierten dagegen findet man gleichmäßige Übergänge.

Abb. 15 : Lenna mit und ohne IFS Codierung
Wegen dieser Eigenschaft hängt auch das Kompressionsverhältnis
von der Vergrößerung, d.h. vom Maßstab der Decodierung
ab. Wenn ein Bild in doppelter, vierfacher usw. Größe
decodiert wird, so wächst das Kompressionsverhältnis
auf das 4-, 16- usw. -fachen an. Denn um das nicht komprimierte
Bild in demselben vergrößertem Maßstab zu speichern,
ist die 4-, 16- usw. fache Menge an Pixeln nötig. Das
Kompressionsverhältnis
variiert also stark, aber es ist nicht sinnvoll, nur auf möglichst
große Kompressionsverhältnisse zu achten. Das decodierte
Bild büßt mit jeder Vergrößerung Genauigkeit
ein und könnte im Extremfall sehr verzerrt wirken. Man muß
sich also auf einen Kompromiß zwischen Kompression und Effizienz
einlassen.
2.2. Bildcodierung - Auffinden des Codes mit
einem Algorithmus
Wie findet man den richtigen Code, d.h. die richtigen Parameter für die Codierung? Dazu ist es nötig, die richtigen Urbildbereiche Di, ihre entsprechenden Abbildungsbereiche und die zugehörige Transformation wi zu bestimmen. Das Wichtigste ist das Auffinden der Urbildbereiche Di oder andersherum das Finden der Bildbereiche Ri .
Dies geschieht mit einem Algorithmus, der verschiedene Teilbereiche auswählt und sie miteinander vergleicht. Die Ähnlichsten ergeben jeweils den Bildbereich Ri und das Urbild Di:
Hier soll nur der Mechanismus, wie das geschehen kann, dargestellt werden. (Für die nötige Effizienz des Alorithmus sind einige Modifikationen möglich und auch nötig.)
Ein Quadratisches Bild wird rekursiv in 4, 16, usw. Teilquadrate zerlegt, bis die Quadrate die Größe von 32x32 Pixeln erreicht haben. Dann stellt man sich eine Kollektion von allen möglichen Teilquadraten D zusammen, die die Größen 8x8, 12x12, 16x16,24x24, 32x32, 48x48 und 64x64 Pixeln besitzen. Nun wird ein erstes 32x32 Pixel-bild Ri mit allen größeren oder gleich großen Teilquadraten D verglichen. Man beachte, daß ein Urbild auch größer sein kann. In diesem Fall muß der Grauwert über die entsprechenden Pixel des Urbildes gemittelt werden, um ein Bild der gleichen Größe wie Ri zu erhalten (z.B. wird bei einem 48x48 Urbild der Wert über 4 Pixel gemittelt, der dann mit dem entsprechendem Wert des Ri -Pixels verglichen werden kann). Haben die Bilder einen gewissen Mindestabstand, sind sie sich also ähnlich genug, so ist eine Paarung (Di ,Ri ) gefunden. Wenn nicht, so wird das 32x32-Pixel Bild in weitere vier 8x8- Pixel Bilder zerlegt, die dann wiederum mit allen größeren oder gleich großen Urbildern D aus der Kollektion verglichen werden.
Auf diese Weise wird ein Bild rekursiv in immer kleinere Teilbereiche Ri zerlegt, bis alle Urbilder gefunden sind. Die rekursive Unterteilung der Ri nennt man auch Quadtree- Methode .
Die entsprechende Transformation wi , die Di in Ri überdührt, wird dann von beiden Bildern Di und Ri selbst bestimmt. Denn es gilt:
Ri = wi (Di) = wi (x,y,z) = (u,v,t).
Damit lassen sich alle Parameter a,b,c,d,e,f,s und o festlegen. Somit ist die Transformation W(P) gefunden, mit der der komplette Bildbereich codiert werden kann.
Zur Decodierung muß man die Abbildung W auf ein beliebiges Anfangsbild P anwenden. Jeder Urbildbereich Di wird dann transformiert und auf seinen entsprechenden Bildbereich Ri abgebildet.
Abb. 16: Lenna nach der 1. , 2. und 10. Iteration
In Abb.16 ist ein Anfangsbild (ein einfaches Raster ), die erste, zweite und 10. Iteration zu sehen. Hier waren Bild- und Urbildbereiche Ri und Di , welche zu vergleichen waren, mit einer festen Größe gewählt. (Di: 16x16 Pixel, Ri: 8x8 Pixel). Nach der ersten und zweiten Iteration kann man noch etwas von dem Raster erkennen. Bei jeder Iteration erscheinen neue Einzelheiten, nach der erste in der Größe 8x8, nach der zweiten in der Größe von 4x4 Pixeln usw. Die 10. Iteration sieht bereits dem Original (siehe Abb. 12) sehr ähnlich. Nur für die Augen war es offenbar schwierig, geeignete Urbildbereiche und Transformatonen zu bestimmen, da sie in dem Bild anscheinend einzigartig sind und keine Ähnlichkeit mit anderen Bildteilen zu finden ist.
Der Hund in Abb.17 ist mit der Quadtreemethode codiert, die Augen
sehen viel runder aus, da kleinere Bildbereiche gewählt werden
konnten.

Abb. 17: Der Hund mit Quadtreemethode Codiert.
Hier zeigt sich, daß die Fraktale Bildkompression eine sehr gute Methode zur Datenreduzierung ist. Es existiert bereits kostengünstige kommerzielle Software wie Images Incorporated, das von Iterated Systems angeboten wird.
Auf der www-Seite http://www.iterated.com findet man Informationen und Demos.
Weiter sei noch ein sehr chönes und verständliches Buch von
Michael F. Barnsley empfohlen, in dem viele Illustrationen
den Text veranschaulichen:
Michael F. Barnsley, Lyman P. Hurd:
Bildkompression mit Fraktalen, Vieweg GmbH Braunschweig/Wiesbaden
,1996
[Peitgen, Fraktale...]:
Peitgen, H.-O.; Jürgens,H.;Saupe, D. :
Fraktale, Bausteine des Chaos, Berlin, NewYork 1992
[Peitgen, Chaos...]:
Peitgen, H.-O.; Jürgens,H.;Saupe, D. :
Chaos: Bausteine der Ordnung, Berlin,1994
[Barnsley, Fraktale...]:
Barnsley,M.: Fraktale:
Theorie und Praxis der Deterministischen
Geometrie, Heidelberg, Berlin, Oxford 1995.
Abbildungsverzeichnis
Abb. 1 : Peitgen, Chaos.....S.519
Abb. 2 : Peitgen, Fraktale ... S. 305
Abb. 3 : - " - S. 306
Abb. 4 : - " - S. 310
Abb. 5 : - " - S. 290
Abb. 6 : - " - S. 291
Abb. 7 : - " - S. 290
Abb. 8 : S. 291
Abb. 9 : Barnsley, Fraktale,.. S. 60
Abb. 10 : Peitgen, Fraktale... S. 332
Abb. 11 : - " - S. 333
Abb. 12 : - " - S. 478
Abb. 13 : - " - S. 480
Abb. 14 : - " - S. 476
Abb. 15 : - " - S. 474
Abb. 16 : - " - S. 487
Abb. 17 : - " -
S. 488