Dilek Altin
1. Begriffserklärung - 'mathematische Fraktale'
2. Prinzip der Rückkoplung und Iteration
3. Zwei Arten mathematischer Fraktale und ihre Eigenschaften
3.1. Klassische Fraktale
3.1.1. Darstellung klassischer Fraktale
3.1.2. fraktale Eigenschaften
3.2. Nichtlineare Fraktale
3.2.1. Die Julia-Mengen - mathematische Anfangsbedingungskarten
3.2.2. Die Mandelbrot-Menge - eine mathematische Parameterlandkarte
3.2.3. Eigenschaften nichtlinearer Fraktale
4. Das Dithering - eine Anwendung mathematischer Fraktale bei der Bildverarbeitung
"Ich prägte den Ausdruck 'fraktal' nach dem lateinischen Adjektiv fractus. Das entsprechende lateinische Verb frangere bedeutet 'brechen': unregelmäßige Fragmente erzeugen. Es ist daher sehr sinnvoll - und kommt unseren Zwecken sehr entgegen -, daß fractus nicht nur 'gebrochen' bedeutet, sondern auch 'unregelmäßig', wobei die beiden Bedeutungen in 'Fragment' bewahrt sind."-Benoit Mandelbrot
Somit ergibt sich direkt der Zusammenhang zu den sogenannten 'mathematischen Fraktalen'. Alle Arten von 'Bildern', die das Ergebnis einer mathematischen Transformation, bei der fraktalen Geometrie handelt es sich um eine iterative Transformation, veranschaulichen und fraktale Eigenschaften aufzeigen, werden unter dem Namen mathematische Fraktale zusammengefaßt.
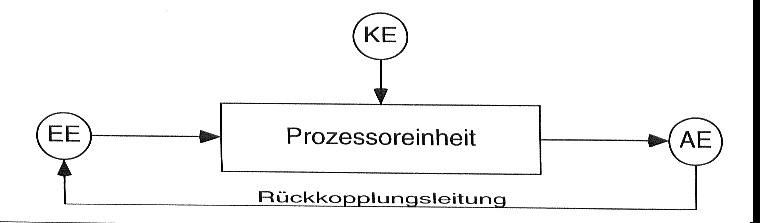
Die Idee der Iteration ist, daß eine Operation wiederholt auszuführen ist, wobei das Ergebnis eines Zyklus (AE) dem nächsten als Eingangswert (EE) zugeführt wird. Wir können solch eine Iteration auch als eine Art 'Rückkoplungsmaschine' betrachten.

Prinzipskizze einer Rückkopplung mit EE=Eingabeeinheit, AE=Ausgabeeinheit, KE=KontrolleinheitDas Verhalten einer solchen Maschine kann durch die Veränderung bzw. Bestimmung von äußeren Einflußgrößen, auch Parameter genannt (KE), gesteuert werden, was - um bei dem Bild der Maschine zu bleiben - in etwa vergleichbar mit dem 'Umschalten' oder 'Regeln' bei einer echten Maschine ist.
Ein berühmtes Beispiel ist die nach Helge von Koch benannte Koch-Kurve.
ABB. 1: Generierung der Koch-Kurve.
zu ABB. 1: Bei der Koch-Kurve ist der Initiator eine gerade Linie. Diese zerlegt man in drei gleiche Teile. Nun wird das mittlere Drittel der Linie entfernt und durch ein gleichseitiges Dreieck so ersetzt, daß die Seitenlänge des Dreiecks der Länge des entfernten Drittels der Grundlinie entspricht. Dies ist bereits die Grundvorschrift zur Konstruktion der Koch-Kurve (Urbild = Generator). Im folgenden Schritt wird wiederum jede verbleibende gerade Strecke in drei gleich Teile untergliedert, und die Prozedur wiederholt sich. Man kann die Iteration prinzipiell solange fortführen, wie es einem die Rechenleistung bzw. die Zeit erlauben. Es ist ersichtlich, daß mit steigender Iterationszahl die Anzahl der Konstruktionsschritte stark anwächst. Tatsächlich ist ein exponentielles Wachstum zu beobachten (bei unserem Beispiel, der Koch-Kurve, entspricht die Anzahl der Linien L = 4^i , wobei unter i die Zahl der Itterationschritte zu verstehen ist.)Neben der Koch-Kurve soll hier noch kurz auf ein weiteres klassisches Fraktal hingwiesen werden, der Hilbert-Kurve, da diese Kurve eine wichtige Rolle bei einer speziellen technischen Anwendung der Fraktale, die im lezten Abschnitt angesprochen wird, spielt.
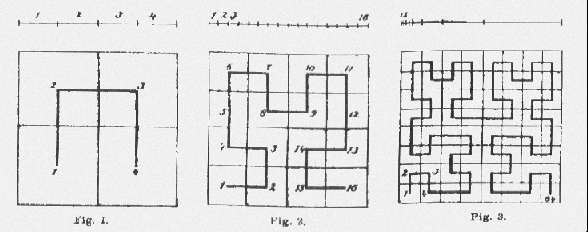
Bei den klassischen Fraktalen spricht man von der exakten Selbstähnlichkeit. Das bedeutet, daß das Fraktal in jeder Vergrößerungsstufe (man kann sich das durch ein Vergrößern oder Verkleinern (Zoomen) des Bildes vorstellen) eine strenge mathematische Ähnlichkeit zu sich selbst aufweist und auch bestimmte Teile der Kurve (z.B. der Generator) sich in ein und demselben Bild ständig, wenn auch in anderen Maßstäben wiederholen. Daraus ergibt sich jedoch auch, daß das Bild der Kurve bei jedem Vergößerungsfaktor ein ähnliches Aussehen hat (wobei allerdings eine gewisse Anzahl von Iterationen vorausgesetzt werden muß, im Idealfall n gegen unendlich, wobei n die Anzahl der Iterationen darstellt). Man spricht hierbei von der Skaleninvarianz einer Kurve (siehe Abb. 3).
ABB. 2: VergrĒŠerung der Koch-Kurve.
zu ABB. 2: Ein Viertel der Koch-Kurve ist um einen Faktor 3 vergrößert. Wegen der Selbstähnlichkeit der Koch-Kurve ist das Ergebnis eine Kopie der gesamten Kurve. Zudem ist die ständige Wiederkehr von Grundelementen im Aufbau der Kurve zu erkennen.
Die berühmtesten Vertreter dieser Gruppe von Fraktalen sind zweifelsohne die Julia-Mengen (Gaston Julia,1893-1978) und die Mandelbrot-Menge (auch M-Menge genannt).
Diese Mengen haben, seitdem sie Mandelbrot Ende der 70er Jahren vorgestellt und somit der Öffentlichkeit zugänglich gemacht hat, einiges an Aufsehen erregt. Sie sind die Geburtsstätten der berühmtesten und schönsten Fraktal-Bilder der Welt. Bis heute haben sie viele Künstler inspiriert, die Wissenschaftler vor immer neue Fragen gestellt und die Öffentlichkeit durch ihre faszinierende Farbenpracht und anmutig wirkende Formenvielfalt magisch angezogen.
x(t+1) = x(t)^2+c
Man kann diese einfache Iterationsgleichung auch wie folgt ausdrücken:
Re(z(t+1)) = Re(z(t))^2-Im(z(t))^2+Re(c)
Im(z(t+1)) = 2*Re(z(t))*Im(z(t))+Im(c)
Bei den Julia-Mengen ist die Größe c eine konstante Anfangsbedingung (Parameter - oder die Schalter bei der Rückkoplungsmaschine!), d.h., daß es für verschiedene c verschiedene Mengen gibt, sogenannte Anfangsbedingungkarten (deshalb auch Plural -> Julia-Mengen). Die Komplexe Eingangsgröße x hingegen ist ein beliebiges Element der komlexen Zahlenebene (anschaulich sind es für uns die Koordinaten eines Pixels (=Bildpunkt) auf dem Computerbildschirm). Nun wird eben dieser beliebige Wert von c in die obige Gleichung eingesetzt und iteriert. Es können jetzt zwei Fälle auftreten:
Bleibt die Iteration begrenzt, so ist das Pixel ein Element der jeweiligen Julia-Menge, und dem Pixel wird eine bestimmte Farbe zugeordnet, z.B. schwarz. Divergiert die Iteration jedoch, so ist dieses Pixel kein Element der Julia-Menge, und ihr wird entweder keine oder, je nachdem, wie schnell sie ins Unendliche divergiert, eine bestimmte andere Farbe zugewiesen, z.B. blau.
Das Ergebnis sind die farbenfrohen Bilder der Julia-Mengen, obwohl hier nochmals darauf hinzuweisen ist, daß eigentlich nur die schwarzen Bereiche der Bilder Elemente der Julia-Mengen sind.
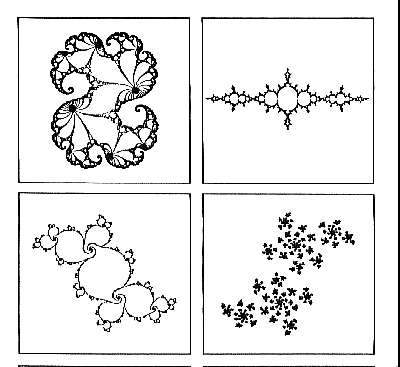
Einige Julia-Mengen(Da kein Achsenbeschriftung auf den Bildern der Julia-Mengen und der Mandelbrot-Menge vorgefunden wurde, folgende Anmerkung: Die horizontale Achse entspricht der reellen und die vertikale Achse der imaginären Achse der komplexen Zahlenebene.)
Die Julia-Menge zeigt für einen bestimmten Parameter das Verhalten der Iterationsfunktion für bestimmte Anfangswertepaare. Sie ist deshalb eine Anfangsbedingungskarte einer nichtlinearen Funktion.
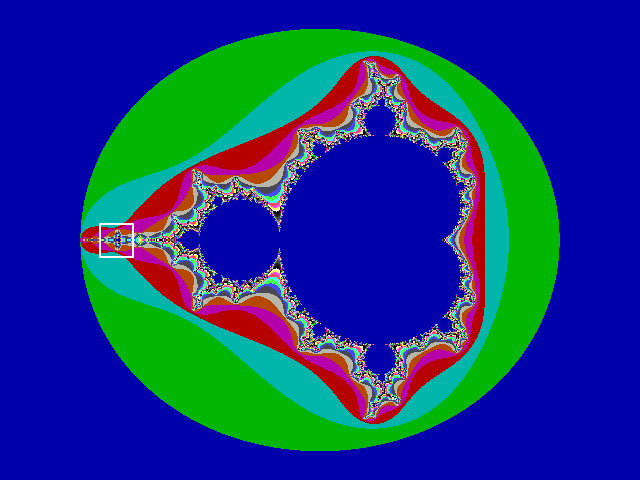
Da die Mandelbrotmenge das Verhalten der Funktion für bestimmte Parameterwerte zeigt, ist sie eine Parameterlandkarte einer nichlinearen Funktion.
Die Ränder der Julia-Mengen und der Mandelbrot-Menge sind unendlich komplex, und man kann zu immer weiteren Details übergehen, indem man den Randbereich herauszoomt (man iteriert für ein abgegrenztes Randgebiet und erhält dadurch eine Vergrößerung dieses Gebietes). Am Rand kann man nun ständig wiederkehrende Formen und Strukturen erkennen, die einander ähnlich zu sein scheinen. Der Begriff 'scheinen' ist hier angebracht, denn es ist keine exakte Selbstähnlichkeit. Man spricht bei dieser Erscheinung von einer statistischen Selbstähnlichkeit. Diese statistische Selbstähnlichkeit wird mit der Tatsache begründet, daß durch Iterationen mit nichtlinearen Gleichungen gewisse 'Verzerrungseffekte' auftreten. Durch diese Verzerrung ist im Rand solcher Mengen ein Meer von Wirbeln verborgen, die ihrerseits von unzähligen dendritischen Armen, kunstvollen Formen und Strukturen umsäumt werden.

Vergrößerung des oben markierten Bereichs der Mandelbrotmenge.Da wir festgestellt haben, daß der Rand solcher Mengen fraktal ist, muß er als solches eine Fraktale Dimension besitzen. Diese beträgt beispielsweise für die Mandelbrot-Menge genau 2.
Zur Wiedergabe von Grautonbildern auf Schwarzweiß-Grafikgeräten, wie z.B. einem Laser- oder einem Tintenstrahldrucker, ist es notwendig, daß der Drucker oder das Programm, welches den Drucker ansteuert, das Grautonbild in ein Bitmap, d.h. in ein Feld von schwarzen und weißen Pixels umwandelt. Um dieses Problem in den Griff zu bekommen, wurden spezielle Algorithmen und Techniken entwickelt, die unter dem Namen 'Dithering' zusammengefaßt werden.
Bei der üblichen Vorgehensweise eines Dithering-Verfahrens wird das Bild linear, entweder Zeile für Zeile oder blockweise, eingelesen und eine Schwarzweiß-Näherung des Bildes erzeugt, wobei darauf geachtet wird, daß der entstehende Fehler so klein wie möglich ist. Das lineare Einlesen und Wiederausgeben hat jedoch zur Folge, daß Spuren des Dithering-Verfahrens zurückbleiben und das Bild für das Auge 'unnatürlich' wirkt.
Genau hier können raumfüllende Kurven wie - speziell in diesem Fall - die Hilbert-Kurve Abhilfe schaffen.
Man projiziert die im Abschnitt 'klassische Fraktale' gezeigte Darstellung der Hilbert-Kurve auf ein Grautonbild und iteriert so oft, daß die Kurve durch alle Pixels dieses Bildes läuft. Die Kurve stellt eine Alternative zum zeilenweisen Einlesen der Pixelblöcke dar.

Das Prinzip des Dithering-Algorithmus, veranschaulicht an vier aufeinanderfolgenden Stufen der Hilbert-Abtastung eines Bildes.
Nun kann das Grautonbild entlang der Hilbert-Kurve durch eine Schwarzweiß-Näherung ersetzt werden, wobei darauf geachtet wird, daß der entstehende Gesamtfehler beim Dithern minimal bleibt.
Der Vorteil dieses fraktalen Dithering-Verfahrens liegt darin, daß im Ersatzbild keine Richtungsmerkmale des Dithering zurückbleiben, wie es beim herkömmlichen 'clustered-dot ordered dither' der Fall war.
Das unregelmäßige Punktmuster, das erzeugt wird, ist für das menschliche Auge wahrnehmungsfreundlicher, zumal es Ähnlichkeiten zur Kornstruktur bei Schwarz-Weiß-Fotografien aufweist.

>>Dithering mit der Hilbert-Kurve (rechts) gegenüber herkömmlichem Dithering (links)
Die hier vorgestellte Anwendung ist wohlgemerkt lediglich eine Variante einer ganzen Gruppe von technischen Anwendungen, wobei sich zugegebenermaßen der Großteil dieser Anwendungen auf Simulationen irgendwelcher physikalischer oder chemischer Vorgänge bezieht, auf die hier nicht näher eingegangen wird.
Nun, es ist leicht erkennbar, daß beide Ansichten höchstwahrscheinlich von Naturwissenschaftlern stammen, denn diese neigen bekanntlich zu extremen Einstellungen gegenüber Neuheiten und haben Schwierigkeiten, sich einer neuen Herausforderung gemäßigt zu nähern.
Tatsache ist, daß durch die fraktale Geometrie der Mathematik ein bisher noch unerforschtes Gebiet in die Hände gefallen ist. Auch ist richtig, daß man sich durch Forschungen auf diesem Gebiet neue Erkenntnisse verhofft, die einen neuen Einblick in die Struktur und Formgebung der Natur geben soll. Aus diesem Grund ist es falsch zu sagen, die Fraktale wären es nicht wert, untersucht zu werden, zumal es heute bereits Ansätze zu ihrer technischen und wissenschaftlichen Anwendung gibt. Man sollte sich aber auch davor hüten, zu viele Hoffnungen in die fraktale Geometrie zu stecken. Wie bei der Chaosforschung stehen wir hier noch am Anfang unserer Erkenntnisse und arbeiten uns langsam voran.
Niemand weiß, was für Erkenntnisse die fraktale Geometrie wirklich mit sich bringen wird. Sie könnte vielleicht doch der Schlüssel zu einer neuen Anschauung unserer Umwelt sein, und aus diesem Grund dürfen wir es uns nicht entgehen lassen, sie gründlich zu studieren, und es wäre falsch, die Augen vor etwas zu verschließen, nur weil es anders ist als sonst!
Sie werden es riskieren, ihre kindlichen Vorstellungen von Wolken, Galaxien, Blättern, Federn, Blumen, Felsen, Bergen, Sturzbächen, Teppichen, Steinen und vielen anderen Dingen zu verlieren. Es wird kein Zurück zu ihrer alten Auffassung dieser Dinge mehr geben.-Michael F. Barnsley